Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 11. 2019 17:09 — Editoval Polopat (02. 11. 2019 17:12)
Entropie směšování ideálních plynů
Zdravím a prosím o pomoc,
snažím se pochopit, co je to vlastně entropie. Při tom jsem na internetu narazil na příklad se směšováním dvou ideálních plynů: Odkaz
Jde o to, že v uzavřené nádobě je přepážkou oddělen plyn A od plynu B. Následně se přepážka odstraní a plyny se smísí. V odkazu je odvozen vzoreček k výpočtu nárůstu entropie. Potud je mi vše jasné.
Zajímá mě, jak by situace vypadala, kdyby plyny A i B byl týž plyn, jen bychom jej na opačných stranách přepážky nějak obarvili barvivem, které nemá vliv na fyzikální vlastnosti plynu, jen by nám umožnilo rozlišovat molekuly, které byly původně na opačných stranách přepážky). Teplota i tlak by tedy všude v nádobě byly před i po smíšení stejné, vlastně by se "nic nestalo", není důvod, aby se odněkud energie přelévala kamkoliv.
Entropie by se ale přesto změnila, a protože entropie je integrál z dQ/T, znamená to, že při konstantní teplotě se někde muselo předat teplo. A tomu právě nerozumím. Kdo komu tady předává teplo? Nebo se žádné nepředává a někde něco přehlížím?
Moc děkuju za případnou radu.
Polopat
Offline
- (téma jako vyřešené označil(a) Polopat)
#6 02. 11. 2019 19:04
Re: Entropie směšování ideálních plynů
Snažit se pochopit entropii na směšování dvou ideálních plynů není zrovna ten nejlepší způsob, z jistého důvodu...(popíšu)
Polopat napsal(a):
Zajímá mě, jak by situace vypadala, kdyby plyny A i B byl týž plyn, jen bychom jej na opačných stranách přepážky nějak obarvili barvivem, které nemá vliv na fyzikální vlastnosti plynu, jen by nám umožnilo rozlišovat molekuly, které byly původně na opačných stranách přepážky).
Jenže takto nemůžeš uvažovat. Buď molekuly od sebe dokážeš rozlišit, nebo je rozlišit nedokážeš. Pokud budou mít stejnou hmotnost a velikost (v klasické kinetické teorii tě jiné vlastnosti nemusejí trápit) tak se jejich smícháním tlak ani teplota nezmění, přesto bude entropie větší.
Hlavní problém s mícháním IDEÁLNÍCH plynů je ten, že pro ně neplatí 3. termodynamický zákon. Ten tvrdí, že když ochladíme plyn (či obecně jakoukoliv látku) na absolutní nulu, tak její entropie bude nulová.
Jenže pro ideální plyn tohle nefunguje. I když ochladíme směs dvou ideálních plynů na absolutní nulu, budou mít pořád tu směsnou entropii, větší než kdyby smíchané nebyly.
Ideální plyny na tohle prostě nejsou vhodné - tenhle model je příliš jednoduchý.
Jinak - zrovna na tohle nejsem žádný velký odborník, řešilo se to kdysi na Aldebaranu (když tam ještě existovalo fórum) - údajně stačí, když použijeme na popis plynu Wan der Waalsovu rovnici a už to funguje. Jenže Wan der Waalsova rovnice je o dost složitější, než stavová rovnice ideálního plynu 
Offline
#7 02. 11. 2019 19:07
Re: Entropie směšování ideálních plynů
Polopat napsal(a):
↑ 2M70:Nemůžu pro to nikde najít podporu. Můžeš mi poslat nějaký odkaz, kdy by to takhle bylo?
Offline
#8 02. 11. 2019 19:17
Re: Entropie směšování ideálních plynů
2M70 napsal(a):
Entropie je, zhruba řečeno, míra neuspořádanosti termodynamického systému a za normálních podmínek může pouze růst, proto znaménku "větší nebo rovno" ve vztahu pro entropii,
Tohle je špatně, ve vzorci je vždycky rovnítko, je to definice entropie.
Má li jít o nevratný děj, musí být celková změna entropie nenulová - a musí to být cyklický proces - tj integrovat se musí přes uzavřenou smyčku - né vždy je to ovšem takto snadné...někdy k tomu musíme nějaké vratné procesy (třeba Carnotovy cykly) doplnit, abychom dostali uzavřený děj.
Třeba přenos tepla vedením - z teplého místa na studené - to je známý nevratný děj ... musíme si představit, že to teplo zase čerpáme zpátky nějakým vratným strojem, abychom měli uzavřený cyklus. Teprve pak je zřejmé, že tímto způsobem "vyrábíme entropii".
Co se mi ale nikde nepodařilo dohledat, proč musí mít nevratné stroje nižší účinnost než ty vratné...
Offline
#9 02. 11. 2019 21:16
#10 02. 11. 2019 23:03
Re: Entropie směšování ideálních plynů
↑ 2M70: V pořádku, děkuju i tak za ochotu pomoci.
↑ MichalAld: Aha, moc děkuju za podnětnou reakci. Chápu tedy, že ideální plyny nejsou ideální k pochopení entropie. Nicméně i když je s nimi problém při absolutní nule, možná v tomto případě bychom k van der Waalsově plynům sahat nemuseli. Jde mi to to teplo. Moje otázka je: když se tedy entropie při smísení zvýší (to bude asi u ideálních i u reálných plynů stejné), znamená to tedy i předávání nějakého tepla, jak to ukazuje rovnice  ?
?
Chování u absolutní nuly nebo vztah růstu entropie k vratným a nevratným dějům s tím myslím přímo nesouvisí - nebo mi ta souvislost uniká? Díky.
Offline
#11 03. 11. 2019 00:05
Re: Entropie směšování ideálních plynů
↑ Polopat:
Skus pozriet sem: https://web.natur.cuni.cz/~zuskova/td2b1_s.pdf
Offline
#12 03. 11. 2019 11:04
Re: Entropie směšování ideálních plynů
↑ Kenniicek: V tom odkazu se vlastně počítá ta směšovací entropie přes Gibbsovu volnou energii, jejíž změna je úměrná změně entropie pro tento jeden případ. Plus se tam konstatuje, že nedochází k žádným tepelným jevům. To mi ale právě není jasné proč.
Entalpie, vnitřní energie, Gibbsova volná energie a jiné termodynamické potenciály jsou vlastně jen veličiny "analogické" vnitřní energii pro různé děje (izotermický, izochorický, ...) - nebo tak to aspoň chápu. Čili to, že se mění Gibbsova volná energie mi vlastně neříká nic jiného, než že se mění energetická bilance toho plynu. Ale na úkor vnitřní energie to asi nebude, když teplota zůstala stejná. Takže to může být jen na úkor předání tepla někam jinam, nebo na úkor práce. Tady mě pak napadá, že ty dva plyny se vlastně rozpínají proto sobě, takže práci konají, ale navzájem se vyruší (jako kdyby jeden plyn posunul píst doleva a druhý zas doprava).
Dává to, co říkám smysl? Případně z čeho tedy plyne, že se žádně tepelné výměny nekonají?
Díky.
Offline
#13 03. 11. 2019 15:28 — Editoval MichalAld (03. 11. 2019 15:39)
Re: Entropie směšování ideálních plynů
Polopat napsal(a):
Moje otázka je: když se tedy entropie při smísení zvýší (to bude asi u ideálních i u reálných plynů stejné), znamená to tedy i předávání nějakého tepla, jak to ukazuje rovnice
?
Chování u absolutní nuly nebo vztah růstu entropie k vratným a nevratným dějům s tím myslím přímo nesouvisí - nebo mi ta souvislost uniká? Díky.
Normálně se to (myšlenkově) dělá tak, že se systém postupně ochlazuje až k absolutní nule (pomocí ideálního - třeba Carnotova - tepelného stroje) a měří se, kolik tepla při které teplotě odevzdá. Tak se dá určit jeho entropie.
U směsi plynů je postupně ochlazuješ až k nule - a reálné plyny by se měly při absolutní nule oddělit samy (nebo dokonale promísit, to já nevím) - při absolutní nule je možný jen jeden jediný stav.
Takže uvažujme, že se při absolutní nule oddělí, ty mezi ně dáš přepážku a pak je zase ohříváš (už oddělené) až je ohřeješ na původní teplotu a tlak. A z rozdílu odebrané a dodané entropie získáš ten rozdíl entropií, co odpovídá těm dvoum stavům.
Zhruba - a podotýkám, že tomu zas tak úplně nekonečně nerozumím...
Ale u ideálního plynu to nejde...ten nic nemotivuje se při 0K smíchat nebo rozdělit...
Další způsob, jak se dohrabat ke změně entropie při smíchání plynů - představ si, že máš přepážku, kterou může jeden z těch plynů procházet a druhý né. Je to trochu ošemetná představa, protože není úplně jisté, jestli taková přepážka může existovat. Ale pokud ano...(pak určitě existuje i druhá přepážka, která zase propouští jen ten první plyn).
Takto můžeš mezi ty dva plyny umístit tyhle dvě přepážky a nechat plyny, ať na ně tlačí. každý bude tlačit na tu svoji a tu druhou ignorovat. Tím že každý z plynů dotlačí tu svoji přepážku až ke stěně, vykonají nějakou práci - a protože je to tepelně izolované, musí se tím nutně snížit vnitřní energie těch plynů - tedy poklesne jim teplota.
No a teď vezmeš topnou spirálu (či Carnotovu tepelnou pumpu) a doplníš chybějící energii pomocí tepla - tím pádem tomu dodáš i entropii (entropie je takové "trochu zpotvořené" teplo...A máš to - kolik entropie jsi musel dodat, tolik by systém získal když bys nechal jeho molekuly jen tak promíchat.
Otázku, jestli se při smíchání dvou "téměř stejných" plynů entropie zvýší nebo né můžeme formulovat také tak, zdali jsme schopní vyrobit tu přepážku, co by jí jeden plyn procházel a druhý né. Nebo obecně, zdali dokážeme ty molekuly nějak rozlišit nebo né. Jestli nám jejich přesun dokáže pohánět nějaký (třeba molekulární) stroj nebo né.
Pokud neexistuje vůbec žádný způsob jak molekuly rozlišit (rozdělit od sebe) tak se entropie pochopitelně nezvýší - jenže my pak nemůžeme tvrdit, že je od sebe dokážeme rozlišit.
Offline
#14 03. 11. 2019 15:35
Re: Entropie směšování ideálních plynů
Předchozí příspěvek využívá jedné důležité vlastnosti entropie - totiž že to je stavová veličina, že její hodnota závisí jen na stavu systému, a né na tom, jak jsme systém do tohoto stavu dostali.
To nám umožňuje určit změnu entropie i při nevratných dějích - tak, že nevratný děj nahradíme vratným, a následným ohřevem či ochlazením. Při vratném ději se entropie nemění a při ohřevu či ochlazování ji dokážeme určit. Tak je také myšlena ta její definice.
To, že je entropie stavová veličina není vůbec samozřejmé (teplo třeba není, a mnoho jiných také ne). Lze to dokázat, ale jen s použitím vyšší matematiky - podstatné totiž je, že entropie je POTENCIÁLEM, tedy že její element je ÚPLNÝM DIFERENCIÁLEM - zvolených stavových proměnných. Potom platí, že její změna nezávisí na integrační cestě.
Schválně jsem tam zmínli to "zvolených stavových proměnných". Entropie zrovna je úplným diferenciálem ve všech možných proměnných, co mohou existovat, ale jiné potenciály to tak nemají (jako třeba známá Entalpie).
Offline
#15 03. 11. 2019 15:41
Re: Entropie směšování ideálních plynů
Jednodušší případ než míchání dvou ideálních plynů je prostě vzít jen jeden ideální plyn, třeba z bomby a nechat jej ucházet do nějakého většího prostoru (třeba místnosti).
Dál je to stejné - nejprve si představíme, že procest provádíme vratně - necháme plyn působit na píst a snižujeme jeho vnitřní energii (entropie se nemění, žádné teplo nedodáváme ani neodebíráme).
A až nám vyplní celou místnost, tak jej ohřejeme na původní teplotu - a máme tu změnu entropie.
Offline
#16 04. 11. 2019 09:32
Re: Entropie směšování ideálních plynů
↑ MichalAld: Aha. Vidím, že je to komplikovanější než jsem myslel a že se nad tím budu muset ještě víc zamyslet (hlavně nad tím ochlazováním k absolutní nule). Ale moc díky za pomoc a podněty, aspoň teď vím, kudy se ubírat, a snad se tam doberu :-).
Díky.
Offline


 a nerovnost je v
a nerovnost je v  ?
?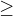 , rovnítko platí pro vratné děje, nerovnítko pro nevratné děje.
, rovnítko platí pro vratné děje, nerovnítko pro nevratné děje.