Matematické Fórum

Počítá se C(n,k), kde k = min(k,n-k).

Vezměme C(13,9) tedy C(13,4).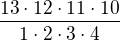



V krocích:
1) 13 ÷ 1 = 13
2) 13 × 12 ÷ 2 = 78; 13 × 12 % 2 = 0, 13 % 2 != 0, 12 % 2 = 0
3) 78 × 11 ÷ 3 = 286; 78 × 11 % 3 = 0, 78 % 3 = 0, 11 % 3 != 0
4) 286 × 10 ÷ 4 = 715; 286 × 10 % 4 = 0, 286 % 4 != 0, 10 % 4 !=0

Lze si tedy všimnout, že v každém kroce je minulý výsledek po pronásobení s aktuálním součinitelem čitatele soudělný s aktuálním součinitelem jmenovatele.

Stejně tak v obráceném pořadí



neboli



V krocích:
1) 10 ÷ 1 = 10
2) 10 × 11 ÷ 2 = 55
3) 55 × 12 ÷ 3 = 220;
4) 220 × 13 ÷ 4 = 715

Jak dokázat, že tato soudělnost platí?

Pod čarou

Kromě tohoto prostého faktu si lze všimnout možností krácení. Např. krok

2) 13 × 12 ÷ 2 = 78 mohl být 13 × 6 = 78.

Podobně krok

4) 220 × 13 ÷ 4 = 715 může být 55 × 13 = 715.

Z toho výplývá, že namísto uvedeného pronásobení, lze někdy pokrátit buď aktuálního součinitele nebo minulý mezivýsledek.