Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 15. 10. 2019 00:03 — Editoval laszky (15. 10. 2019 00:08)
Re: Binomial sum
![$\sum^{n-1}_{i=0}\sum^{n}_{j=i+1}\!\bigg(\!j\binom{n}{i}+i\binom{n}{j}\!\bigg)=\sum^{n}_{j=1}\sum^{j-1}_{i=0}\!\bigg(\!j\binom{n}{i}+i\binom{n}{j}\!\bigg) = \frac{1}{2} \left[\sum^{n-1}_{i=0}\sum^{n}_{j=i+1}\!\bigg(\!j\binom{n}{i}+i\binom{n}{j}\!\bigg) + \sum^{n}_{i=1}\sum^{i-1}_{j=0}\!\bigg(\!j\binom{n}{i}+i\binom{n}{j}\!\bigg)\! \right] = $](/mathtex/c3/c300b15d8a0fae7f2c2f8a766febe414.gif "kopírovat do textarea")
![$= \frac{1}{2} \left[ \sum^{n}_{i=0}\sum^{n}_{j=0} \bigg(j\binom{n}{i}+i\binom{n}{j}\bigg) - 2\sum^{n}_{i=0}i\binom{n}{i}\right] = \frac{1}{2} \left[ 2\sum^{n}_{i=0}\sum^{n}_{j=0}i\binom{n}{j}- 2\sum^{n}_{i=0}i\binom{n}{i}\right] = 2^n\sum_{i=0}^{n}i - \sum_{i=1}^n n \binom{n-1}{i-1} =$](/mathtex/da/dac2c7002b4f08ef475caa228465ff44.gif "kopírovat do textarea")
Offline
#5 20. 11. 2019 09:26 — Editoval Marian (20. 11. 2019 09:33)
Re: Binomial sum
↑ byk7:
I don't know the story you are talking about. However, I suggest the following approach that seems to be rather trivial.
![$
\sum_{i=0}^{n-1}\sum_{j=i+1}^{n}\left [j\binom{n}{i}+i\binom{n}{j}\right ]
&=\sum_{i=0}^{n-1}\binom{n}{i}\sum_{j=i+1}^{n}j+\sum_{i=0}^{n-1}\sum_{j=i+1}^{n}i\binom{n}{j}\\[3mm]
&=\underbrace{\frac{1}{2}\cdot\sum_{\vphantom{j}i=0}^{n-1}\binom{n}{i}\cdot (n-i)\cdot (n+i+1)}_{S_1}+\underbrace{\frac{1}{2}\cdot\sum_{j=1}^{n}\binom{n}{j}\cdot j\cdot (j-1)}_{S_2}.
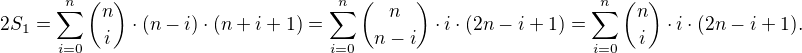
$](/mathtex/81/817a7cf1eff5c4b2a20b05bf13b3c603.gif "kopírovat do textarea")
.
![$\boldsymbol{\sum_{i=0}^{n-1}\sum_{j=i+1}^{n}\left [j\binom{n}{i}+i\binom{n}{j}\right ]=n^2\cdot 2^{n-1}}.$](/mathtex/ea/ea01b691d0d06f221fe5ae0ba0e94c26.gif "kopírovat do textarea")
Offline