Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Algoritmy a programování
- » Nalezení výrazných bodů na křivce (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 11. 2019 07:47 — Editoval Karmanova cesta (17. 11. 2019 07:56)
- Karmanova cesta

- Příspěvky: 62
- Reputace: 0
Nalezení výrazných bodů na křivce
Připravuji program pro analýzu hlasu, který píšu v Delphi a řeším tam situaci, kdy mám dvě křivky. První je křivka purpurová, která je výsledkem autokorelace, druhá křivka je fialová jako výsledek frekvenční analýzy. Připomínám, že nejsem žádný matematik, v matematice na ZŠ jsem sotva prošel, jediný vzorec, který si pamatuju a kterému rozumím je pythagorova věta, potažmo možná zvládu pochopit ještě goniometrické funkce. Tady moje znalosti matematiky končí. Spíš se věnuju logickému uvažování a tvorbě algoritmu.
Zde jsem si připravil obrázky z Audacity:
Odkaz
Na prvním obrázku je tedy purpurová křivka, ze které bych chtěl nejdříve dostat žlutou křivku, která představuje zjednodušení. Původní křivka má více bodů a cílem nové křivky je zredukovat množství dat, abych získal hrubou představu o křivce (ty data pak mohu později zahrnout do algoritmu programu). Takže bych chtěl nalézt body, které se nachází výrazně nahoře (červená barva) nebo výrazně dole (modrá barva). Přitom je ale pro mě také důležité celkově počítat i s tou délkou žluté čáry, protože pokud je čára delší tak je významnější. Naopak, když by byla čára příliš krátká (třeba jen půl čtverce) tak už pro mě není zajimavá.
Budu moc rád, pokud mi dáte nějaký vzorec (i když vzorcům moc nerozumím) nebo napíšete pseudo kód. Pokud tu někdo rád pracuje s Mathlabem tak by to taky bylo dobré. Zatím žádné konkrétní data k dispozici nemám, zde jsem udělal vzorek pomocí mikrofonu v Audacity, při 16b audiu 22kHz mono jsem nahrál zvuk písmene "B".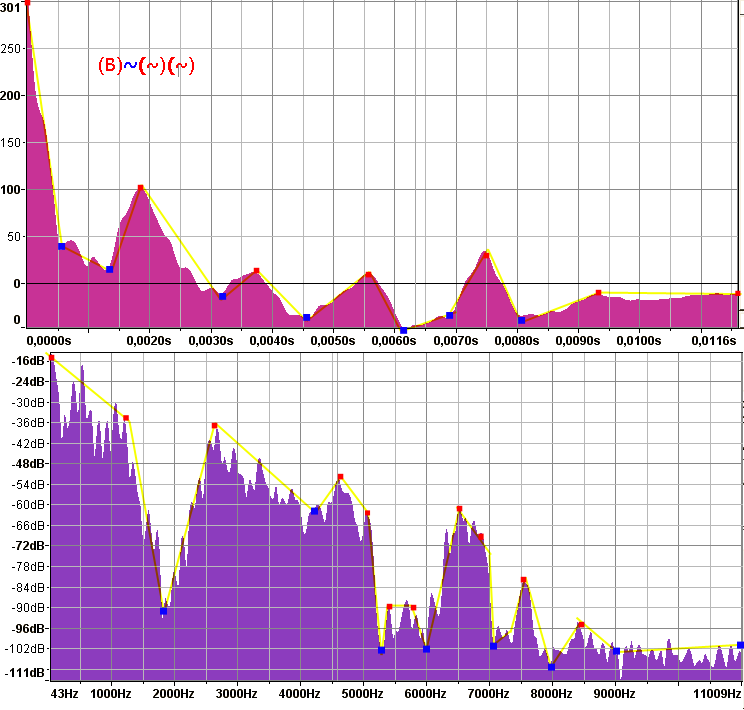
U spodního grafu bych to chtěl udělat podobně.
Grafů může být více a myslím, že pro mě není tak podstatná přesná úroveň hlasitosti v dB jako spíš tvar křivky. Hlasitost nahrání se přeci jen může lišit a mě jde spíš o to, abych dokázal rozpoznat tvar křivky u určitého písmene vysloveného na nahrávce zvuku, než aktuální hlasitost nahrávky. Proto by bylo ideální kdyby výsledek byl například v procentech nebo v desetinném čísle od 0,0 - 1,0. Zároveň však potřebuju podle něčeho poznat jestli ten bod patří k těm horním nebo k těm dolním.
PS:
U prvního grafu na dolní ose jsou jednotky s (nevím proč tomu tak je), protože mě vlastně zajímá stupnice, tónina či frekvence.
Offline
- (téma jako vyřešené označil(a) jarrro)
#2 17. 11. 2019 09:17
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení výrazných bodů na křivce
Ahoj,
a jaké máš požadavky na tvar té žluté křivky? Všiml jsem si např., že chceš, aby procházela význačnými peaky (maximy i minimy). Máš nějaké kritarium, kdy dané maximum/minimum ignorovat a kdy jím má žlutá křivka procházet?
"Máte úhel beta." "No to nemám."
Offline
#3 17. 11. 2019 11:30 — Editoval Karmanova cesta (17. 11. 2019 11:38)
- Karmanova cesta

- Příspěvky: 62
- Reputace: 0
Re: Nalezení výrazných bodů na křivce
↑ check_drummer:
Omlouvám se, tak jsem se nevyjádřil dost jasně.
Ta žlutá křivka tam je jenom, abych zvýraznil co chci udělat.
Mě jde jen o to, získat ty červené a modré body, to jsou ty "význačné peaky", což jsem v nadpisu vlákna pojmenoval jako "výrazné body". Já nevěděl, jaký je pro to formální název. Já tomu říkal taky "hlavní body". Prostě ty výrazné amplitudy. Žlutá křivka už je jen pro efekt. Je ale fakt, že výpočtem délky žluté přímky člověk získává důležitou informaci o tom, jak je ta křivka v daném místě výrazná.
Vůbec nemám žádný vzorec, nevím jak se taková věc dělá. Jen mě napadá:
Asi je třeba nejdříve najít nejvyšší bod a potom od toho bodu hledat bod nejnižší, který je v dostatečné vzdálenosti po žluté přímce od toho nejvyššího bodu.
Offline
#4 17. 11. 2019 16:44
Re: Nalezení výrazných bodů na křivce
Zdravím, pokud data vyfiltruji, pak změny směru mi ukáží, kde mám ty body hledat.
Offline
#5 17. 11. 2019 19:04
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení výrazných bodů na křivce
↑ Karmanova cesta:
Ale ty nemáš označen každý "vrchol", ale jen některé. Jaká máš tedy kriteria pro to, že daný vrchol je pro tebe důležitý?
Jinak obecně vrchol (maximum) získáš tak, že jeho hodnota je větší než hodnota obou jeho sousedních bodů. Tak ale získáš i celkem nepodstatné vrcholy (rovněž v obrázku výše neprochází žlutá křivka všemi vrcholy), tak je potřeba stanovit, jaké vrcholy jsou pro tebe důležité.
Možná by třeba bylo možné říct, že vrchol považujeme za důležitý, když je jeho hodnota větší než hodnota všech bodů do vzdálenosti k bodů od něj, kde k je zvoleno vhodně.
"Máte úhel beta." "No to nemám."
Offline
#6 18. 11. 2019 02:16 — Editoval Karmanova cesta (18. 11. 2019 02:44)
- Karmanova cesta

- Příspěvky: 62
- Reputace: 0
Re: Nalezení výrazných bodů na křivce
Mák:
Nehledám průměr. Snažím se o to, aby moje křivka procházela těmy extrémy. Ke dvé datové linii jsem přikreslil nejdříve žlutou křivku, která by ty data mohla zjednodušit při první operaci a kdybychom to opakovali dostali bychom ještě jednodušší křivku purpurovou.
check_drummer:
Každý vrchol není označen proto, že se nejedná o extrém. Jestli jde o extrémní výkyv posuzuju nejen podle vetikální vzdálenosti/délky, ale i podle horizontální vzdálenosti/délky.
Jde tam taky o to, že ta křivka by se neměla zjednodušit příliš, aby nedošlo k posunutí čáry nesprávným směrem.


Na posledním obrázku se snažím vysvětlit proč nechci aby zmizely ty velké žluté plochy. Protože když budu mít nějaké podobné křivky (význačné body), které budu chtít mezi sebou porovnat (porovnat křivky mezi sebou) tak ten bod bude třeba malinko posunutý doprava nebo doleva nebo bude mít trochu jinou výšku
Tak nevím jestli vám ty obrázky k něčemu pomohly. Jak se na to teď dívám tak vidím dvě možnosti jak to realizovat:
Buďto:
A) hledat ty nejvyšší body a ty neposouvat dolů; dolní body pokud je to nutné trochu posunout nahoru, aby nedošlo ke ztrátě žlutých ploch. Tím pádem mi spodní body slouží jako dolní mez, kterou potřebuji v daném místě na ose x znát.
nebo:
B) hledat ty nejvyšší body a ty neposouvat dolů; dolní body neposouvat nahoru, čímž může dojít ke ztrátě žlutých bodů, ale záse budu mít zachovánu informaci o tom jak nízko to až může zajít.
Myslím, že pro mě je vhodnější řešení A) protože když budu porovnávat křivky tak u toho dolního bodu budu posuzovat zda nepřekračuje ten spodní limit. Informace extrémních výkyvech v dolních bodech taky není k zahození. Ale pokud bych se měl rozhodnout pro jedno řešení, tak A.
Offline
#7 18. 11. 2019 03:09 — Editoval Karmanova cesta (18. 11. 2019 03:10)
- Karmanova cesta

- Příspěvky: 62
- Reputace: 0
Re: Nalezení výrazných bodů na křivce
↑ check_drummer:
No právě, jestli ten vrchol zahrnu nebo ne, závisí na délce té čáry. Čím delší je ta spojnice, tím významnější ten body bude. Když je spojnice menší než polovina čtverce tak nový bod nevytvářím.
Na prvním obrázku mezi prvním modrým (a) a druhým modrým bodem (b) jsem se rozhodl nezahrnovat ty dva vrcholy mezi nimi protože u prvního ten bod je moc blízko prvnímu modrému bodu a u druhého vrcholu, ten leží velmi blízko přímce/spojnici, čímž odpadá potřeba ho vykreslovat.
Pak je tam jedno místo (?) na 0,0015s kde si nejsem jistý zda vytvořit bod. Vzhledem k tomu, aby nebyla oseknuta ta plocha tak bych ho vytvořil, ale zase záleží na délce čáry (c).
Takže tu vidím dva faktory: jedním je délka čáry a druhým je vzdálenost vrcholu od čáry.

Ke světle modrému popisku: tam má být "příliš malá vzdálenost od spojnice"
Pak je tam spojnice z červeného bodu na 0,0020s až modrý bod na 0,0030s - ten bod jsem si dovolil trochu opravit a posunul jsem ho doleva, aby spojnice byla blíže vrcholům, čímž se nevytvoří bod u vrcholů d, e.
Další spojnice u vrcholů f,g tam se taky nevytváří body protože jsou blízko spojnici.
Offline
#8 18. 11. 2019 16:44
Re: Nalezení výrazných bodů na křivce
Vítej ve světě UI (Umělé Inteligence)...jak jsi zajisté už zjistil, není to žádná prdel...
Problém samozřejmě není, jak to naprogramovat, ale vymyslet nějaký univerzální popis, čím jsou ty vyznačené body specifické.
Na první pokus bych zkusil něco ve stylu "kvazi-lokálního extrému", jestli to tak můžu nazvat. Tj hledat maximum, nebo minimum, ovšem v nějakém předem stanoveném rozsahu.
Taky můžeš před tím na křivku aplikovat nějaký digitální filtr.
Otázka ovšem je, jestli to bude dělat zrovna to co potřebuješ. Není až takový problém vymyslet postup, co bude fungovat zrovna na té tvé jedné křivce. Ovšem - má li to fungovat na tisícovce křivek - to už je mnohem větší problém.
Na podobné úlohy lze také vyzkoušet neuronové sítě ...
Offline
#9 18. 11. 2019 18:53 — Editoval Karmanova cesta (18. 11. 2019 18:56)
- Karmanova cesta

- Příspěvky: 62
- Reputace: 0
Re: Nalezení výrazných bodů na křivce
Pojem "kvazi-lokální systém" mi nic neříká, ale pokud něco takového existuje potřebuju znát i anglický název abych mohl prohledat internet.
Tak k výpočtu vzdálenosti od modrého bodu k bodu "a" použiju pythagorovu větu.
Jak ale spočítat vzdálenost bodu "b" od žluté spojnice? Vím že toto se v matematice používá, ale já si nepamatuju ani název natož vzorec. Vím, je to taky pythagorova věta, jenže jak najít průsečík s odvěsnou?
Počet křivek možná tisíc.
V knihovně je filtr sinch a Chebyshev, což ale nevím zda je využitelné:
http://files.dreamdev.org.ru/_hdd/_proj … s-pas.html
Offline
#10 18. 11. 2019 21:20
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení výrazných bodů na křivce
↑ Karmanova cesta:
Proč např. spojuješ bod a s bodem b a nespojíš ho s druhým maximem nacházejícím se mezi body a,b? - toto maximum je už přece dostatečně daleko od bodu a... K čemu se chci dobrat - zda je možné sestrojit algoritmus, který postupně prochází ta maxima/minima a když najde nějaké dostatečně daleko od naposled přidaného, tak ho prostě přidá...
"Máte úhel beta." "No to nemám."
Offline
#11 18. 11. 2019 21:29 — Editoval Karmanova cesta (18. 11. 2019 21:56)
- Karmanova cesta

- Příspěvky: 62
- Reputace: 0
Re: Nalezení výrazných bodů na křivce
check_drummer:
a, b jsou vrcholy (červenou barvou textu jsem označil vrcholy).
Ty myslíš první a druhý modrý bod.
"Proč např. spojuješ bod a s bodem b a nespojíš ho s druhým maximem nacházejícím se mezi body a,b? - toto maximum je už přece dostatečně daleko od bodu a..."
To jsem už vysvětloval. Je tam druhá podmínka, která zahrnuje vzdálenost vrcholu od té žluté čáry, kterou hledám.
Ještě jednou se podívej na ten velký obrázek, je tam napsáno 1) světle červený text a za 2) světle modrý text. Světle modrá šípka ukazuje na vzdálenost mezi druhým vrcholem a tou čárou.
Jde o to spočítat délku světle modré čáry. To se dá udělat pomocí pythagorovy věty a goniometrických funkcí:
Offline
#12 19. 11. 2019 20:04
- Karmanova cesta

- Příspěvky: 62
- Reputace: 0
Re: Nalezení výrazných bodů na křivce
Teď jsem zjistil, že anglicky se těm horním (červeným) a dolním (modrým) význačným bodům říká envelope:
https://en.wikipedia.org/wiki/Envelope_(waves)
Tak jsem zase o něco moudřejší.
Jak se tomu říká česky to nevím.
Offline
#14 21. 11. 2019 00:53
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení výrazných bodů na křivce
↑ Karmanova cesta:
Ahoj, spíše než jen ta maxima je envelope celá křivka spojující tyto body.
"Máte úhel beta." "No to nemám."
Offline
#15 21. 11. 2019 00:56
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení výrazných bodů na křivce
↑ Karmanova cesta:
Proč teda vůbec bod b zařazuješ do té žluté čáry? Proč bod a nespojit s tím druhým růžovým maximem a bod b nevynechat?
"Máte úhel beta." "No to nemám."
Offline
#16 21. 11. 2019 14:58
- Karmanova cesta

- Příspěvky: 62
- Reputace: 0
Re: Nalezení výrazných bodů na křivce
Vrchol b přece neleží na žluté čáře. Na posledním obrázku přece vidíš zelenou čáru, která vede od středu té žluté čáry k vrcholu. Jestli ti jde o ten druhý modrý bod na obrázku prvním v tomto vlákně, tak ten leží naopak pod vrcholem b, tedy v extrému (v dolní obálce).
Offline
#17 22. 11. 2019 17:08
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení výrazných bodů na křivce
↑ Karmanova cesta:
Tak si ty body označme: ty modré body nazvěme c,d, maxima mezi nimi jsou tedy a,b a pro úplnost ještě oznčme e minimum mezi maximy a,b.
A můj dotaz tedy zní - proč spojuješ bod c právě s bodem d a ne např. s bodem b nebo s bodem e? Bodem d přece nemusí žlutá křivka procházet..
"Máte úhel beta." "No to nemám."
Offline
#18 22. 11. 2019 17:31 — Editoval Karmanova cesta (22. 11. 2019 19:32)
- Karmanova cesta

- Příspěvky: 62
- Reputace: 0
Re: Nalezení výrazných bodů na křivce
Já bych řekl, že je to podle toho, že posuzuju o jak velkou plochu bych přišel, kdybych tu čáru udělal jinde. Na jednom obrázku výše jsem udělal žluté plochy, o které bych přišel. Když ta žlutá plochá je velká, tak posouvám bod nahoru, aby byla zahrnuta. Tady se mi zdá, že když jak jsem to nakreslil na prvním obrázku je to ideální, protože to je blízké k tomu tvaru, který je na křivce.
Další věc:
Je třeba tam mít jakési okno a podívat se dál dopředu.
Bod e se mi zdá taky jako dobrý kandidát, ale vedle něj existuje ještě d, který je taky dobrý.
Jak se rozhodnout mezi těma bodama bodama?
Já myslím, že je to podle délky té žluté čáry, že čím je delší, tím je to lépe. Snažím se přece o to, abych co nejvíce redukoval množství bodů, takže proč tam cpát body navíc pokud nejsou třeba? Tím, že se podívám dopředu a zjistím, které body mohu použít, z nich si vyberu ten nejvzdálenější. A stále platí že se v této fázi hledá minimum, takže další bod to už být nemůže, protože se jedná o vrchol.
Ten proces hledání bodů v dolní obálce bude o tom, že člověk musí furt porovnávat vzdálenosti a vyhodnocovat, jestli je malá nebo velká. Když je malá, nemá pro mě bod význam, když je velká, tak význam má, pokud se nejedná o bod z horní obálky.
Tuším, že ten proces porovnávání směrem dopředu se nazývá "okno". Okno je limitováno tím, že mohu hledat jen v jedné obálce, nemohu přeskakovat z obálky do obálky.
Nesmím zapomenout na posuzování plochy u toho následujícího vrcholu - asi bych se vyhnul složitým kalkulacím s výpočtem plochy a měřil bych poměr součtu délky línií křivky (modré a zelené čáry) mezi vrcholy s délkou k spojnice k vrcholu (oranžová barva).
Na tomto obrázku posuzuji, zda je bod d vhodný kandidát na spojení s bodem c.
Offline
#19 22. 11. 2019 21:32
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení výrazných bodů na křivce
↑ Karmanova cesta:
Máš tam dvě kriteria, která chceš splnit - mít ty žluté úsečky co nejdelší a minimalizovat "chybu", ta kriteria jdou ale často proti sobě - s krátkou úsečkou budeš mít často menší chybu a s delší naopak. takže musíš mít nějaké pravidlo, které rozhodne, jaké kriterium v daném případě rozhodne.
Jak definuješ velikost chyby té aproximace?
Když se díváš tím oknem řekněme k bodů dopředu, tak se ale může stát, že by bylo nejvhodnější spojit poslední bod s tím k+1-ním, který ale už v okně nemáš, a tak nebude odhad optimální (to je ale asi jasné).
Také by v některých případech bylo vhodnější neuvažovat jen maxima a minima, ale i nějaké další body - abys získal co nejlepší aproximaci (a relativně malý počet žlutých úseček).
"Máte úhel beta." "No to nemám."
Offline
#20 24. 11. 2019 15:03 — Editoval Karmanova cesta (24. 11. 2019 15:04)
- Karmanova cesta

- Příspěvky: 62
- Reputace: 0
Re: Nalezení výrazných bodů na křivce
Dostáváme se už dost daleko do teoretických detailů a mě teoretické uvažování moc nejde. Musel bych to naprogramovat a pak bych uviděl. V současnosti jsem ale práci na programu zastavil, protože během čtení ze souboru wave se mi vyskytla chyba, se kterou si neumím poradit.
Offline
#21 24. 11. 2019 19:54
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Nalezení výrazných bodů na křivce
↑ Karmanova cesta:
Když hledáš nějakou aproximaci tak obecně máš proti sobě dvě kriteria - aby ta aproximace byla co nejjednodušší a aby byla co nejpřesnější, a je nutné zvolit nějaký kompromis mezi nimi.
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Algoritmy a programování
- » Nalezení výrazných bodů na křivce (TOTO TÉMA JE VYŘEŠENÉ)
