Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vlastnosti lineární (ne)závislosti - (ne)závislost samotného vektoru
#1 02. 12. 2019 18:28
Vlastnosti lineární (ne)závislosti - (ne)závislost samotného vektoru
Ahoj,
mel bych dotaz ze zakladu linearni algebry. Ve skriptech "Uvod do algebry, zejmena linearni" - Petr Olsak (http://petr.olsak.net/ftp/olsak/linal/linal.pdf) jsou na str. 26 uvedeny "Základní vlastnosti lineární (ne)závislosti" (Věta 2.17). Chtel bych se zeptat na vlastnost cislo 6, ktera zni:
Samotný vektor  (chápaný ovšem jako skupina vektorů o jednom prvku) je lineárně nezávislý právě tehdy, když je nenulový.
(chápaný ovšem jako skupina vektorů o jednom prvku) je lineárně nezávislý právě tehdy, když je nenulový.
Muj dotaz:
Jak muze byt samotny vektor nezavisly? O nekolik stranek drive se pise, ze ma smysl se bavit pouze o skupine vektoru, pokud se bavime o linearni (ne)zavislosti vektorů (viz. Poznamka 2.11 na str. 19). Jestli tomu rozumim dobre, tak to znamena, ze ma smysl se bavit o linearni (ne)zavislosti pouze tehdy, mame-li k dispozici minimalne 2 vektory. Nerozumim textu v zavorce u Vety 2.17, ze vektor je chapany jako skupina vektoru o jednom prvku. Tomu teda vubec nerozumim.
Pomuze mi to nekdo prosim vysvetlit?
A.
Offline
#2 02. 12. 2019 18:43
Re: Vlastnosti lineární (ne)závislosti - (ne)závislost samotného vektoru
↑ Andrew123:
Ahoj, to plyne z defineice linearni nezavislosti:
Skupina vektoru 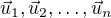 je linearne nezavisla prave tehdy, kdyz plati implikace
je linearne nezavisla prave tehdy, kdyz plati implikace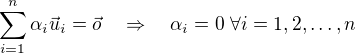
No a pro libovolny nenulovy vektor  plati:
plati: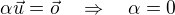 ,
,
takze  je linearne nezavisly.
je linearne nezavisly.
Offline
#4 02. 12. 2019 19:14
Re: Vlastnosti lineární (ne)závislosti - (ne)závislost samotného vektoru
↑ misaH:
Ahoj,
ze 1 vektor tvori jednoprvkovou skupinu, tak tomu samozrejme rozumim.. Linearni (ne)zavislost jsem ale chapal, ze je to vlastnost mezi vektory (viz ta poznamka 2.11), Predstavoval jsem si to analogicky k necemu jako je napr. usporadani prirozenych cisel. Tj. pokud mam jedno cislo, tak nemuzu rici, ze je jedno vetsi/mensi, kdyz nemam k dispozici druhe cislo.., protoze k porovnani cisel je potreba mit minimalne 2 cisla, jedno cislo nestaci a je to malo. Takhle jsem uvazoval a nerikam, ze jsem uvazoval dobre..:-)
Offline
#5 02. 12. 2019 19:19
Re: Vlastnosti lineární (ne)závislosti - (ne)závislost samotného vektoru
↑ laszky:
Super, dik za vysvetleni.
Mozna jeste doplnujici otazka..
Muze byt samotny vektor take zavisly? Predpokladam, ze ano a to tehdy, kdyz je nulovy, protoze existuje netrivilani linearni kombinace, ktera je rovna nulovemu vektoru. Je to tak?
Offline
#6 02. 12. 2019 21:23
Re: Vlastnosti lineární (ne)závislosti - (ne)závislost samotného vektoru
↑ Andrew123: Nezávislost jednoho vektoru asi nemá žádnou rozumnou interpretaci, podobně jako třeba součet 0 čísel. Někdy je ale dobré mít tyhle speciální případy rozumně definované, aby je člověk nemusel stále nějak speciálně ošetřovat. Abys mohl např. říkat "nechť A je množina nezávislých vektorů" místo "nechť A je množina nezávislých vektorů nebo obsahuje právě jeden vektor a ten není nulový".
Offline
#7 03. 12. 2019 00:10
Re: Vlastnosti lineární (ne)závislosti - (ne)závislost samotného vektoru
↑ Stýv:
Jo jo, asi jako když máme hrst věcí, které jsou stejné - a chceme to rozšířit i na případ, kdy máme jen jednu (stejnou) věc...
(jen jdu kolem a nějak mě to napadlo....)
Offline
#8 03. 12. 2019 09:29
Re: Vlastnosti lineární (ne)závislosti - (ne)závislost samotného vektoru
Ahoj ↑ MichalAld:,
Akoze nejaky vyrok, alebo jeho kontrapozovany vyrok su ekvivalentne, tak pouzit jeden alebo druhy je bezne.
A v tomto cviceni, niekomu sa ten kontrapozovany vyrok moze zdat viac intuitivny.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 03. 12. 2019 11:32 — Editoval Rumburak (03. 12. 2019 13:15)
Re: Vlastnosti lineární (ne)závislosti - (ne)závislost samotného vektoru
↑ Andrew123:
Ahoj. Uvedu jiště jiný pohled na zmíněnou problematiku:
Základním pojmem je zde seznam prvků (v našem případě vektorů), tedy jakási konečná či
nekonečná posloupnost. Seznam může být jednoprvkový i prázdný, konkretní prvek se v něm
může vyskytovat i vícekrát (tj. na různých posicích). Jdeme-li na pojem lineární závislosti vektorů
přes jejich seznamy (snad je zřejmé jak), potom nejasnosti, o kterých píšeš, nevzniknou.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vlastnosti lineární (ne)závislosti - (ne)závislost samotného vektoru
