Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Důkaz - teorie grafů pomocí eulerova vztahu, problém s nerovností
#1 07. 12. 2019 13:10
- Matezu

- Příspěvky: 41
- Škola: VŠB-TUO, Fakulta elektrotechniky a informatiky
- Pozice: Student
- Reputace: 0
Důkaz - teorie grafů pomocí eulerova vztahu, problém s nerovností
Zdravím, pracuji na důkazu jednoho tvrzení z teorie grafů a k tomu budu nejspíše potřebovat využít toto tvrzení (téměř jistě).
Jednoduchý rovinný graf na  vrcholech má nejvýše
vrcholech má nejvýše 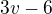 hran.
hran.
Důkaz: Můžeme předpokládat, že graf je souvislý, jinak bychom mohli přidat další hrany. V daném grafu G označíme počet stěn f a počet hran h. Jelikož graf neobsahuje smyčky ani násobné hrany, je každá stěna (v libovolném nakreslení grafu G) ohraničena alespoň 3 hranami. Každou hranu na hranici oblasti započítáme nejvýše dvakrát (ve dvou přilehlých stěnách). Platí tedy  .
.
Vím, jak vypadá eulerův vzorec  . Já ale nějak prostě nejsem schopný rozluštit, jak se přišlo na nerovnost
. Já ale nějak prostě nejsem schopný rozluštit, jak se přišlo na nerovnost  . Každá stěna je ohraničena alespoň 3 hranami z důvodu, že 3-cyklus je nejmenší cyklus, který dokáže graf rozdělit na dvě stěny. To však znamená, že když budeme mít méně než 3 hrany, bude stěna zajisté jen 1. Zato pokud budeme mít 3 nebo více hran, tak graf bude mít 1 nebo více stěn. Proto nechápu, proč ta nerovnost nevypadá
. Každá stěna je ohraničena alespoň 3 hranami z důvodu, že 3-cyklus je nejmenší cyklus, který dokáže graf rozdělit na dvě stěny. To však znamená, že když budeme mít méně než 3 hrany, bude stěna zajisté jen 1. Zato pokud budeme mít 3 nebo více hran, tak graf bude mít 1 nebo více stěn. Proto nechápu, proč ta nerovnost nevypadá  nebo
nebo 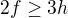 . Asi nějak nechápu, co ta nerovnost představuje, když mi nedává smysl ani věta "Každou hranu na hranici oblasti započítáme nejvýše dvakrát". Jak můžeme jednu hranu počítat dvakrát?
. Asi nějak nechápu, co ta nerovnost představuje, když mi nedává smysl ani věta "Každou hranu na hranici oblasti započítáme nejvýše dvakrát". Jak můžeme jednu hranu počítat dvakrát?
Mohli byste mě, někdo, prosím naťuknout správným směrem? Děkuji
Offline
#2 07. 12. 2019 13:37
Re: Důkaz - teorie grafů pomocí eulerova vztahu, problém s nerovností
↑ Matezu:
Ahoj, v rovinnem grafu jsou dva typy hran. Ty ktere tvori hranici mezi dvema stenami (mnozina  ) a ty, ktere netvori hranici mezi dvema stenami (mnozina
) a ty, ktere netvori hranici mezi dvema stenami (mnozina  ). Velikost noziny
). Velikost noziny  muzeme odhadnout pomoci poctu sten. Protoze kazda stena je ohranicena minimalne tremi hranami, plati
muzeme odhadnout pomoci poctu sten. Protoze kazda stena je ohranicena minimalne tremi hranami, plati
Cislo 3f musime vydelit 2, protoze kazda hrana z  lezi ve dvou stenach a pocitali bychom ji tedy dvakrat. Celkem proto plati
lezi ve dvou stenach a pocitali bychom ji tedy dvakrat. Celkem proto plati
Takze 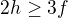 .
.
Poznamka: Napriklad graf ve tvaru hvezdy (vsechny hrany maji jeden spolecny vrchol) je rovinny graf, ktery ma libovolny pocet hran, ale jen jednu stenu.
Je tedy jasne, ze pokud existuje nejaka nerovnost mezi h a f, musi byt tvaru 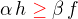 .
.
Offline
#3 07. 12. 2019 13:50
- Matezu

- Příspěvky: 41
- Škola: VŠB-TUO, Fakulta elektrotechniky a informatiky
- Pozice: Student
- Reputace: 0
Re: Důkaz - teorie grafů pomocí eulerova vztahu, problém s nerovností
↑ laszky:
Díky moc, konečně mi to vlezlo do hlavy, stačilo se na to podívat z trošku jiného úhlu.
Jinak v mém případě jde o 2-souvislý rovinný graf s obvodem minimálně 6, takže množina hran, které neoddělují dvě stěny je 0. Samozřejmě v mém důkaze nebude figurovat fakt, že stěny oddělují minimálně 3 hrany, ale 6 hran, ale principiálně je to stejné. Ještě jednou děkuji
Offline
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Důkaz - teorie grafů pomocí eulerova vztahu, problém s nerovností