Matematické Fórum

Pozitron

Dobrý den,
Dnes nám dala paní učitelka v prváku na střední dala zajímavý příklad, mě zabral asi hodinu, má být řešitelný bez kalkulačky, ale pokud ji požijete tak vám ušetří asi patnáct minut počítání.
Zadání: mějme číslo 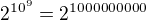$2^{10^{9}} = 2^{1000000000}$ určete jeho posledních pět cifer. (jednoty, desítky ...)

Nápověda 1:

Autor skryl část textu. Zobrazit/skrýt!

Pokud máte nějaký časově efektivnější postup tak se o něj neváhejte podělit.

Ferdish

Autor skryl část textu. Zobrazit/skrýt!

edison · 09. 12. 2019 01:02

Pro Android existuje program jménem myslím Math tricks, různé dost vysoké mocniny a vysvětlení jak je počítat se tam vyskytují hodně.

check_drummer · 09. 12. 2019 21:12

↑ Pozitron:
Ahoj, proč myslíš že je tvůj postup neefektivní?

Pozitron · 09. 12. 2019 21:53

↑ check_drummer:
Protože mi učitelka řekla že je to zajímavé řešení, ale není optimální. A to její "lepší" mi nechce ukázat ať na něj přijdu sám.

laszky · 09. 12. 2019 22:58

↑ Pozitron:

Ahoj, mozna by to mohlo jit takto:

Mocniny dvojky stridaji celkem 4 posledni cislice 2,4,8,6.
Poslednich dvojic je celkem 20: vsechna delitelna 4 (tj 25) minus 5 koncicich na 0.
Podobne poslednich trojic je 100, ctveric 500 a petic 2500.
Protoze se opakuji cyklicky (a $10^9/2500=400000$ ), stacilo by ti spocitat poslednich pet cifer cisla $2^{2500}$ .
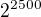I to je vsak pracne.
Co je vsak jasne je, ze kdyz cislo 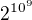$2^{10^9}$ respektive 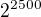$2^{2500}$ vynasobis dvema,
musi se cyklus vratit na zacatek a vysledne cislo tak musi koncit dvojkou.
Kdyz znovu vynasobis dvema, musi cislo koncit 04, kdyz znovu dvema, tak musi koncit 008,
kdyz znovu dvema, tak cislo konci 0016 a kdyz jeste jednou dvema, tak cislo konci 00032.
Z toho uz jde odvodit, ze cislo 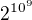$2^{10^9}$ konci na... (zabere to 2-3 minutky)

Autor skryl část textu. Zobrazit/skrýt!

check_drummer · 11. 12. 2019 13:43

↑ laszky:
Ahoj, nesmíš použít úvahy týkající se mod 10000 ani práci s modulem. To vše si myslím skytě děláš, když uvažuješ cyklické posloupnosti. :-) Ale myslím, že byl ten zákaz příliš restriktivní.

check_drummer · 11. 12. 2019 13:48

↑ laszky:
Ahoj ještě jednou, a je těmi podmínkami (po vynásobení 4 končí na 04, apod.) už to koncové pětičíslí určeno jednoznačně?

check_drummer · 11. 12. 2019 13:52

laszky napsal(a):
Poslednich dvojic je celkem 20: vsechna delitelna 4 (tj 25) minus 5 koncicich na 0.

Jak víš, že se všechny takovéto dvojice dvojice (dělitelné 4) mocninami dvojky nabývají?

laszky · 11. 12. 2019 14:33 — Editoval laszky (11. 12. 2019 14:34)

↑ check_drummer:

Ahoj. K te jednoznacnosti: Cisla (koncici na 6), ktera kdyz vynasobis 4 tak konci na 04, jsou celkem dvou typu: Bud konci na 26, nebo na 76. Cisla koncici na 26 ale muzes vyloucit, ptz nejsou delitelna 4. Obdobne se postupuje pro 008, 0016 a 00032.

To nabyvani mocnin by slo asi dokazat sporem... Napr. predpokladejme, ze mocnina cisla 2 nikdy nekonci na 48, potom ale mocnina 2 nikdy nekonci na 24, pak nemuze koncit ani na 12, ani na 56, ani na 28,...

check_drummer

laszky napsal(a):
↑ check_drummer:
To nabyvani mocnin by slo asi dokazat sporem... Napr. predpokladejme, ze mocnina cisla 2 nikdy nekonci na 48, potom ale mocnina 2 nikdy nekonci na 24, pak nemuze koncit ani na 12, ani na 56, ani na 28,...

Ale to už je vlastně výčet všech možností, protože můžeš zkoumat ty dvojice do té doby než nenarazíš na dvojici na kterou může mocnina končit, což může být i dost dlouhý řetězec. Stejně tak můžeš ty mocniny vyjádřit a zjistit kolik dvojčíslí opravdu je. Nešlo by to nějak elegantněji, např. že 100 má v rozkladu 25 a nsd(2,25)=1? a že 25 je druhá mocnina prvočísla? Třeba přes malou Fermatovu větu.

vanok · 14. 12. 2019 10:39 — Editoval vanok (14. 12. 2019 10:50)

Ahoj ↑ check_drummer:,
Myslim si ze pojem modulo je velmi prirodzeny a asi kazdy stredoskolak ho pouziva v beznom zivote. ( uz aj cas sa casto vyjadruje modulo 12, ci 24, uhlova miera v °, modulo 360 atd)
Inac konstatacia, ze 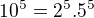$10^5=2^5.5^5$ moze byt vyhodne pouzita na riesenie problemu (ak riesitel vie nieco o Eulerovej funkcii).

Inac ako naznacil kolega Laszky(Pozdravujem) pre riesitela cvicenia, moze byt uzitocne, ze dlzka periody poslednych m cislllic daneho cisla je $4.5^{m-1}$ , ak by chcel prehlbit pouzite vlasnosti v rieseni, ktore kolega popisal.

Matematické Fórum

#1 08. 12. 2019 23:07 — Editoval Pozitron (08. 12. 2019 23:09)

určení posledních pěti číslic

#2 08. 12. 2019 23:42 — Editoval Ferdish (08. 12. 2019 23:46)

Re: určení posledních pěti číslic

#3 09. 12. 2019 01:02

Re: určení posledních pěti číslic

#4 09. 12. 2019 21:12

Re: určení posledních pěti číslic

#5 09. 12. 2019 21:53

Re: určení posledních pěti číslic

#6 09. 12. 2019 22:58

Re: určení posledních pěti číslic

#7 11. 12. 2019 13:43

Re: určení posledních pěti číslic

#8 11. 12. 2019 13:48

Re: určení posledních pěti číslic

#9 11. 12. 2019 13:52

Re: určení posledních pěti číslic

laszky napsal(a):

#10 11. 12. 2019 14:33 — Editoval laszky (11. 12. 2019 14:34)

Re: určení posledních pěti číslic

#11 12. 12. 2019 22:03 — Editoval check_drummer (12. 12. 2019 23:49)

Re: určení posledních pěti číslic

laszky napsal(a):

#12 14. 12. 2019 10:39 — Editoval vanok (14. 12. 2019 10:50)

Re: určení posledních pěti číslic

Zápatí