Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Algoritmy a programování
- » Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
#1 14. 12. 2019 19:31 — Editoval Uživatel919 (14. 12. 2019 19:35)
- Uživatel919

- Zelenáč
- Příspěvky: 11
- Reputace: 0
Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
Pracuji na příkladu 1.2.5 z Průvodce labyrintem algoritmů.
Je jasné (a také dané – viz str. 463), že je potřeba užít metodu 2 jezdců. Nicméně posloupnost není uspořádaná.
Zadání
Součet úseku: Je dána posloupnost 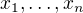 kladných čísel a číslo s. Hledáme i a j taková, že
kladných čísel a číslo s. Hledáme i a j taková, že  . Navrhněte co nejefektivnější algoritmus.
. Navrhněte co nejefektivnější algoritmus.
Není mi jasné, jak by metoda 2 jezdců mohla pracovat s neuspořádanou posloupností.
Mé řešení:
Code:
void Hledej(IList<int> posloupnost, int hledanýSoučet)
{
int
i = 0,
j = posloupnost.Count - 1,
suma,
index;
bool sumaJeNižší;
while (i < j)
{
suma = 0;
sumaJeNižší = true;
for (index = i; index <= j && sumaJeNižší; ++index)
{
suma += posloupnost[index];
sumaJeNižší = suma < hledanýSoučet;
}
if (suma == hledanýSoučet)
{
Console.WriteLine($"Interval <{i},{index - 1}>.");
break;
}
else if(sumaJeNižší)
{
Console.WriteLine("Úsek nenalezen.");
break;
}
else // suma > hledanýSoučet
{
++i;
}
}
}Uteklo mi něco?
Offline
#2 15. 12. 2019 12:53
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
↑ Uživatel919:
Ahoj, nevidím, kde snižuješ index j. Asi by bylo lepší popsat algoritmus slovy.
"Máte úhel beta." "No to nemám."
Offline
#3 15. 12. 2019 14:11 — Editoval Uživatel919 (15. 12. 2019 14:13)
- Uživatel919

- Zelenáč
- Příspěvky: 11
- Reputace: 0
Re: Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
↑ check_drummer:↑ check_drummer:
Index j právě nesnižuju, protože posloupnost není uspořádaná, tzn., že snížením j bych mohl zahodit nižší číslo místo vyššího.
To je to, co mě zajímalo, ale asi to mám dobře a zbytečně se ptám.
Offline
#4 15. 12. 2019 16:24
Re: Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
↑ Uživatel919: Ty prohledáváš všechny možnosti, což určitě není nejefektivnější. Nevidím důvod, proč by metoda dvou jezdců neměla fungovat. Akorát ti jezdci oba začnou v 0. ;-)
Offline
#5 15. 12. 2019 17:48 — Editoval Uživatel919 (15. 12. 2019 17:54)
- Uživatel919

- Zelenáč
- Příspěvky: 11
- Reputace: 0
Re: Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
↑ Stýv:
Aha, díky. Vlastně to tam mám. Akorát vždycky napočítávám od začátku. Správně tedy při mezisoučet > součet odečtu 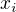 . Jinak v opačném případě přičtu
. Jinak v opačném případě přičtu  . (Samozřejmě inkrementuji.)
. (Samozřejmě inkrementuji.)
Offline
#6 16. 12. 2019 20:02
Re: Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
Tvůj úsek kódu
Code:
for (index = i; index <= j && sumaJeNižší; ++index)
{
suma += posloupnost[index];
sumaJeNižší = suma < hledanýSoučet;
}je určitě lepší psát takto (protože je na první pohled vidět, co to vlastně dělá):
Code:
for (index = i; index <= j; ++index)
{
suma += posloupnost[index];
if(suma > hledanýSoučet)
break;
}Další věc je, že by to chtělo někam ukládat ty indexy, to že najdeš součet je super, ale stejně nakonec nevíš kde.
Použití názvu proměnné "j" mi přijde dost nešťastné, když se vlastně k ničemu nepoužívá - jsi tam mohl rovnou nechat to posloupinost.Lenght.
Pokud jde o rychlost - takto ty součty počítáš pořád znova a znova ... v "ideálním" případě je budeš počítat n-krát a skončíš na poslední variantě i = lenght. Určitě to lze udělat i tak, že si dílčí součty někam uložíš a pak je jen upravuješ...ale jestli to bude opravdu rychlejší, to já nevím...
Offline
#7 16. 12. 2019 21:57
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
↑ Uživatel919:
Chápu to dobře, že musí být i<=j a že přesněji hledáme tato i,j taková, že  ?
?
"Máte úhel beta." "No to nemám."
Offline
#8 16. 12. 2019 22:01
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
↑ Uživatel919:
Co to je metoda 2 jezdců?
"Máte úhel beta." "No to nemám."
Offline
#9 17. 12. 2019 00:50
Re: Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
Podle reakce ↑ Uživatel919: bych řekl, že otázka je dostatečně zodpovězena kolegou ↑ Stýv:em. Detaily k metodě dvou jezdců jsou k dohledání v textu odkazovaném v prvním příspěvku (ačkoli je otázka, jestli si to zaslouží pojmenování).
Offline
#10 18. 12. 2019 09:52
- check_drummer

- Příspěvky: 5452
- Reputace: 106
Re: Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
Stýv napsal(a):
Nevidím důvod, proč by metoda dvou jezdců neměla fungovat. Akorát ti jezdci oba začnou v 0. ;-)
Ahoj, a jak konkrétně by ti jezdci měli jezdit? V původní metodě dvou jezdců se index i zvětšoval a index j zmenšoval? Nyní se tedy budou indexy pouze zvětšovat? Když bude součet menší než s, zvětší se j a když větší než s, zvětší se i?
"Máte úhel beta." "No to nemám."
Offline
#11 18. 12. 2019 11:04
#12 18. 12. 2019 11:05
- Uživatel919

- Zelenáč
- Příspěvky: 11
- Reputace: 0
Re: Součet úseku neuspořádané posloupnosti (PLA 1.2.5)
↑ check_drummer:
Již řečeno Stývem. Pojedou oba od nuly. Zbytek je více méně stejný.
Offline
Stránky: 1
- Hlavní strana
- » Algoritmy a programování
- » Součet úseku neuspořádané posloupnosti (PLA 1.2.5)