Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 19. 12. 2019 14:23
#4 19. 12. 2019 14:47
#6 19. 12. 2019 15:25 — Editoval laszky (19. 12. 2019 15:27)
Re: oskulacni kruznice
↑ Missskkka:
Znas prusecik s osou y, tj bod ![kopírovat do textarea $[x_0,f(x_0)]=[0,1]$](/mathtex/b5/b5b078f85ac2bf3a98b0fa21a00b1a5f.gif) , spocitej
, spocitej 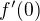 a
a 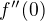 a z toho spocitej souradnice stredu
a z toho spocitej souradnice stredu ![kopírovat do textarea $[a,b]$](/mathtex/4a/4ab4b4c56d5423829b45e9ed06c42c5b.gif) a polomer kruznice
a polomer kruznice  .
.
Offline

 v jejim pruseciku s osou y. dekuji
v jejim pruseciku s osou y. dekuji