Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 01. 2020 00:24
Nerovnosti; ukaž / dokaž
Dobrý den.
Pro kladná čísla 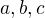 ukažte:
ukažte:
Dospěl jsem k: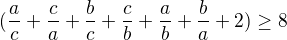
Což je při 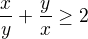 pro každá
pro každá 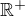 pravda.
pravda.
Nyní mám ale rozhodnout, zda nerovnost platí i pro jakékoli reálná čísla.
Jediné co mě napadlo:
Pokud pro  platí, že:
platí, že: 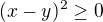 , pak nerovnost neplatí, protože nejmenší číslo, které můžu dostat na levé straně je
, pak nerovnost neplatí, protože nejmenší číslo, které můžu dostat na levé straně je  .
.
Nejsem si vůbec jistý, zda je to správně.
Tyhle věci nejsou ze školy, učím se dokazování / ukazování nerovnic sám, proto se omlouvám za nejasnosti nebo špatné pojmy.
Děkuji.
Offline
#4 13. 01. 2020 08:56 — Editoval vanok (14. 01. 2020 03:00)
Re: Nerovnosti; ukaž / dokaž
Ahoj ↑ 6c6f6c: ,
Poznamka:
Na dokaz tvojej nerovnosti mozes pouzit tieto 3 nerovnosti ( pre a,b,c kladne)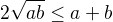

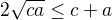
( ktore vies iste sam dokazat)
tak, ze urobis ich sucin.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 13. 01. 2020 12:14
Re: Nerovnosti; ukaž / dokaž
↑ 6c6f6c:
> A co jsem tím přesně zjistil?
Přesně jsi tím zjistil to, že zadaná nerovnost neplatí pro libovolná reálná čísla. Jinak řečeno, předpoklad o kladnosti čísel a, b, c nemůže být vynechán.
> Jde to dokázat i jinak než dosazením?
Čistě teoreticky bys mohl zkusit nerovnost považovat za nerovnici a najít všechny trojice reálných čísel, které to splňují. Ale proč bys to dělal? Úkolem je rozhodnout, jestli pro "libovolná (ne nutně kladná) reálná čísla platí nerovnost". Už víš, že platí pro kladná. Tak se budeš dívat např. na to, když jedno číslo bude záporné. No a po chvilce hraní si nebo za použití nějaké zkušenosti by se mělo zdát jasné, že toto platit nebude. Takže stačí najít jediný protipříklad, který jsi už našel. (Mimochodem, není nutné nulovat kteroukoliv ze stran, lazsky to navrhl proto, že se protipříklad hledá jednodušeji. Ale těch je celá řada, další třeba a=-2, b=1, c=18.)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#6 13. 01. 2020 13:09
Re: Nerovnosti; ukaž / dokaž
Dobře, co když by 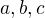 ale mohlo být záporné pouze v nějakým intervalu? Mohl bys mě nakopnout nějakým nápadem na tvoje "Čistě teoreticky" prosím?
ale mohlo být záporné pouze v nějakým intervalu? Mohl bys mě nakopnout nějakým nápadem na tvoje "Čistě teoreticky" prosím?
vanok; snažil jsem se nějak najít ty nerovnice, ale nedaří se. Jmenuje se ten důkaz nějak?
Offline
#7 13. 01. 2020 15:51
Re: Nerovnosti; ukaž / dokaž
Ahoj ↑ 6c6f6c:,
mozes vyuzit, ze 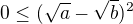 a jej podobne nerovnosti.
a jej podobne nerovnosti.
Ze to dokazes!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 13. 01. 2020 21:59 — Editoval vanok (13. 01. 2020 22:00)
Re: Nerovnosti; ukaž / dokaž
Ahoj ↑ 6c6f6c:, to mne odpovedas ?
Ja som cakal, ze napises toto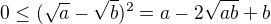
co je ekvivalentne z 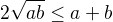 .....a analogicky pre ostatne 2 nerovnosti.
.....a analogicky pre ostatne 2 nerovnosti.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 13. 01. 2020 22:17
Re: Nerovnosti; ukaž / dokaž
Jžš, udělal jsem početní chybu v jednom z kroků, děkuju, k tomu jsem se taky dostal.
A co teď tedy vím, že nemůžu dosadit jakékoli reálné číslo, ale pouze v intervalu  ?
?
Kdy  :
: 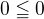
A jakékoli reálné číslo menší než nula mi dá nerovnost.
Offline
#12 13. 01. 2020 22:29
Re: Nerovnosti; ukaž / dokaž
↑ 6c6f6c:,
Nie, to dokazuje, ze nerovnost plati pre lubovolne kladne cisla.
( a specialne to da rovnost pre 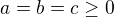 . ).
. ).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 13. 01. 2020 23:09
Re: Nerovnosti; ukaž / dokaž
↑ 6c6f6c:
Zdá se mi, že po roznásobení všech závorek dostaneš
Dále máme dokázat 
My ale víme, že např první člen z těchto tří lze odhadnout  .
.
Víš proč, poznáváš něco v tom?
tg(x) je funkcí života.Jednou jsi nahoře🗽, podruhé zas dole 🗿.
Offline
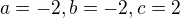

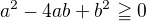 .
. .
.