Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 01. 2020 17:50
Inverzni funkce - dukaz vlastnosti
Ahoj,
resim 2 dukazy tykajici se tematu inverzni funkce. Oba si jsou podobne a snad i kratke, tak to snad muze byt tady v jednom dotazu.. Vzhledem k tomu, ze v ucebnici je pouze zadani a neni reseni, tak bych zde chtel nekoho poprosit, zda by mi to mohl zkontrolovat, jestli je to dobre, ci zda by nenalezl elegantnejsi reseni. Me reseni se mi zdaji totiz prilis jednoduche..
Dokazte, ze plati:
a) Funkce  je prosta.
je prosta.
b) Je-li funkce  rostouci, pak je i
rostouci, pak je i  rostouci.
rostouci.
Me reseni:
a) Funkce inverzni je definova pouze pro proste funkce. Pro  plati
plati 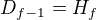 a
a 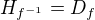 . Jinymi slovy, prohodil jsem jen dve osy, a protoze jednomu
. Jinymi slovy, prohodil jsem jen dve osy, a protoze jednomu 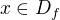 bylo prirazeno pouze jedno
bylo prirazeno pouze jedno 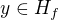 , tak to musi platit i obracene pro
, tak to musi platit i obracene pro  , coz je vlastne definice proste funkce. Tim je dukaz hotov.
, coz je vlastne definice proste funkce. Tim je dukaz hotov.
b) Funkce  je rostouci, prave kdyz pro vsechna
je rostouci, prave kdyz pro vsechna 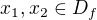 plati: Je-li
plati: Je-li  , pak
, pak  . Protoze pro inverzni funkci jenom obratime osy, tak bude pro
. Protoze pro inverzni funkci jenom obratime osy, tak bude pro  platit nasledujici: Je-li
platit nasledujici: Je-li  , pak
, pak  . Coz je definice rostouci funkce, cili plati, ze inverzni funkce
. Coz je definice rostouci funkce, cili plati, ze inverzni funkce  k rostouci funkci
k rostouci funkci  je opet rostouci.
je opet rostouci.
Me reseni mi prijdou jako samozrejme, ze to snad neni ani potreba psat a mozna to proto neni uplne dobre... Slo by to vice rozepsat nebo znate nejake lepsi reseni?
Diky moc
A.
Offline

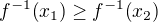 potom z rastúcosti f a definície inverznej funkcie máme
potom z rastúcosti f a definície inverznej funkcie máme