Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » kontrakce (antisimetrické) 3-formy vektorem
#1 15. 01. 2020 19:53
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
kontrakce (antisimetrické) 3-formy vektorem
Dobrý den,
prosím o pomoc:
hledám li kontrakci 2formy vektorem (vnitřní součin), postupuji takto: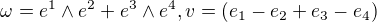
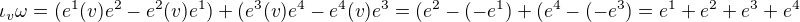
jak ale budu postupovat v případě 3 formy?
např::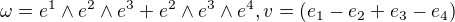
zkoušel jsem vypočítat kontrakci 2 formy krát kontrakci jedna formy a vyšly mě odlišné výsledky, když jsem počítal nejdříve první dva prvky a nebo nejdříve druhé dva prvky vnějšího součinu.
Děkuji za rady
Offline
#2 16. 01. 2020 07:36
- Roscelinius
- Příspěvky: 51
- Škola: FEKT
- Reputace: 0
Re: kontrakce (antisimetrické) 3-formy vektorem
je toto mé řešení správné?
užil jsem vzorec: 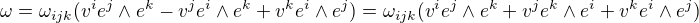
tedy:
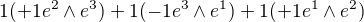
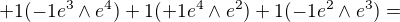
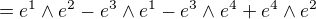
Mohl by mi někdo říci jaký je význam kontrakce diferenciální formy s vektorem? Ve většině učebnic je o tom jen zmínka a jak se s tím počítá v druhé dimenzi, plus obecný vzorec. Uniká mi praktické užití. Prý elementární práce je kontrakce pole s objemovým elementem. Dokázal by mi někdo přiblížit souvisosti?
Děkuji.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » kontrakce (antisimetrické) 3-formy vektorem