Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 19. 01. 2020 16:52 — Editoval vlado_bb (19. 01. 2020 16:53)
Re: Konvergencia
↑ jajko: V casti  ide o bodovu konvergenciu, ano? Odpoved je velmi jednoducha - aky je ale tvoj nazor?
ide o bodovu konvergenciu, ano? Odpoved je velmi jednoducha - aky je ale tvoj nazor?
A este k textu ulohy - ide o ohranicenu postupnost funkcii, alebo postupnost ohranicenych funkcii? Lebo pri tej druhej moznosti by bola uloha zaujimavejsia.
Offline
#3 19. 01. 2020 17:03 — Editoval jajko (19. 01. 2020 17:08)
Re: Konvergencia
↑ vlado_bb: myslím si, že b je pravdivé ale pri a mám pochybnosti, skôr by som povedal, že nie vždy to platí
A skôr asi ide o ohraničenú postupnosť funkcií
Offline
#7 19. 01. 2020 17:56
Re: Konvergencia
↑ vlado_bb: nepodarilo sa mi nájsť príklad. Bude to taktiež pravda? Su správne úvahy, že ak existuje limita ohraničenej postupnosti funkcií v bode x a má sa rovnať funkčnej hodnote v bode x tak aj daná funkcia musí byť ohraničená?
Offline
#9 19. 01. 2020 18:11
Re: Konvergencia
↑ vlado_bb: ak by teda šlo o postupnosť ohraničených funkcií, tak neboli by aj tak obidve možnosti správne?
Offline
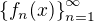 je ohraničená
je ohraničená
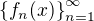 je ohranicena, ak ...
je ohranicena, ak ...
 je pravda. Pokial ide o
je pravda. Pokial ide o