Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 01. 2020 19:10
- uršulka_life

- Příspěvky: 46
- Reputace: 1
Adam a Bohouš- slovní úloha
Dobrý večer, mohl by jste mi prosím někdo pomoci s touto úlohou? Adam a Bohouš se zúčastnili turnaje hraného systémem každý s každým, v němž každý hráč měl odehrát 1 zápas denně. Adam a Bohouš jako jediní onemocněli a nedokončili turnaj. Bohouš odstoupil o 5 dni dříve než Adam. Celkem se odehrálo 350 zápasů. Kolik jich odehrál Adam? Hrál s Bohoušem?
Já mám totiž problém porozumět tomu, že najednou co Bohouš odstoupil byl lichý počet hráčů, a jak tedy mohl každý odehrát 1 zapas za den? Nebo hrál jeden člověk ty zápasy 2? Nebo někdo vůbec nehrál?
Offline
- (téma jako vyřešené označil(a) uršulka_life)
#2 23. 01. 2020 19:35
Re: Adam a Bohouš- slovní úloha
↑ uršulka_life:
Zdravím.
Možná je to v tom, že podle zadání
" ... každý hráč měl odehrát 1 zápas denně."
ale není řečeno, že jej po odchodu Bohouše v následujících pěti dnech každý skutečně odehrál.
Pokud se tedy nemýlím.
Offline
#3 23. 01. 2020 19:37
Re: Adam a Bohouš- slovní úloha
↑ uršulka_life:
Ahoj. Souhlasim s ↑ Jj:. Rekl bych, ze v planu bylo, aby kazdy odehral jeden zapas denne. Po odstoupeni Bohouse se proste jeho naplanovane zapasy nehraly. To same s Adamem.
Napoveda: To cislo 350 ti da nejake omezeni na celkovy pocet hracu.
Offline
#4 23. 01. 2020 19:37 Příspěvek uživatele uršulka_life byl skryt uživatelem uršulka_life. Důvod: Pozdě přečteny komentář
#6 23. 01. 2020 23:00
Re: Adam a Bohouš- slovní úloha
No já jsem teda asi blbej, ale žádné řešení jsem nenašel. Podle mě to ani řešení nemá. Jde o soustavu  , kde
, kde  je počet dnů, kdy byl nemocný Adam, a
je počet dnů, kdy byl nemocný Adam, a  je počet hráčů. Jde vlastně o celočíselné řešení na kousky paraboly, který je definován na intervalu obsahující jediné celé číslo, a to
je počet hráčů. Jde vlastně o celočíselné řešení na kousky paraboly, který je definován na intervalu obsahující jediné celé číslo, a to  . Ale to by pak byl plán 378 utkání a od toho nejde odečíst celočíselně
. Ale to by pak byl plán 378 utkání a od toho nejde odečíst celočíselně 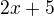 , aby to dalo 350...
, aby to dalo 350...
Pletu se v něčem?
Offline
#7 24. 01. 2020 06:24
Re: Adam a Bohouš- slovní úloha
↑ surovec:
Já se vůbec nevyznám v sestavování rozpisů turnajů a tudíž neumím s jistotou zvážit možné souvislosti. Ale řekl bych, že výpočty nemusí být až tak přímočaré, že něco může napovídat poslední věta textu úlohy.
Na každý jednotlivý zápas musí být dva hráči. Odstoupí-li Bohouš, je v dalších dnech zřejmě o jeden zápas méně a některý z hráčů v návaznosti na rozpis "pauzíruje". Odstoupí-li ještě Adam, může myslím být v dalších dnech o dva zápasy méně, nebo taky jen o jeden - v den, kdy podle rozpisu mají hrát spolu (pokud tedy spolu ještě nehráli).
Třeba by se dal průběh turnaje zkombinovat tak, aby se podmínkám úlohy vyhovělo.
Pokud se tedy nemýlím.
Offline
#8 24. 01. 2020 08:00
Re: Adam a Bohouš- slovní úloha
↑ surovec:
To by platilo, kdyby spolu A s B už hráli než jeden z nich onemocněl. Ale kdyby ještě nehráli?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#9 24. 01. 2020 08:52 Příspěvek uživatele surovec byl skryt uživatelem surovec. Důvod: Reakce měla být na Zdenek1
#10 24. 01. 2020 08:57
Re: Adam a Bohouš- slovní úloha
↑ zdenek1:
No jo, to je ono. Pokud by spolu už hráli, je to ta situace, co jsem popsal - nemělo by to celočíselné řešení. Takže spolu ještě nehráli, a tím se ta soustava změní na  . A ta má celočíselné řešení
. A ta má celočíselné řešení  . Hezká úložka!!!
. Hezká úložka!!!
Offline
#11 24. 01. 2020 11:39
- uršulka_life

- Příspěvky: 46
- Reputace: 1
Re: Adam a Bohouš- slovní úloha
No já jsem to potom řešila tak ze jsem si řekla kolik zápasu by se nehrálo kdyby spolu hráli, nebo kdyby spolu nehráli,a to jsem odecetla od plánovaného počtu.
Děkuji za rady
Offline
