Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 01. 02. 2020 20:04 — Editoval Meglun (01. 02. 2020 20:04)
Re: inflexní body
↑ vlado_bb:
osamostatnim si  , u polynomu mi to jde, ale tady mi vadi to
, u polynomu mi to jde, ale tady mi vadi to 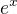 . Nevim jak s tim vyrazem pracovat.
. Nevim jak s tim vyrazem pracovat.
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
#5 01. 02. 2020 20:09 — Editoval Meglun (01. 02. 2020 20:10)
Re: inflexní body
↑ vlado_bb: pardon
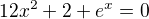
stale je tam to 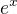
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
#7 01. 02. 2020 20:13
Re: inflexní body
↑ vlado_bb:
aha na prvni pohled ne, ale z puvodniho vyrazu Odkaz
se v jistem bode meni z konkavniho do konvexniho tvaru
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline
#8 01. 02. 2020 20:16
Re: inflexní body
↑ vlado_bb: uz jsem si toho vsiml, nemeni se a je konvexni cely
Společnost tě může připravit o všechno, ale to co máš v hlavě, ti nikdo neveme.
Offline


 a nevim jak na to jit
a nevim jak na to jit