Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 02. 2020 16:37 — Editoval stuart clark (01. 02. 2020 16:37)
- stuart clark

- Příspěvky: 1015
- Reputace: 7
polynomials
Consider the equation in terms of  as
as  for real number
for real number 
The sum of non real roots can be 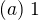

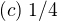
 None.
None.
also evaluation of minimum number of non real roots of the equation is
Offline

