Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Počet k-místých čísel s ciferným součtem n
#1 26. 05. 2014 16:15
Počet k-místých čísel s ciferným součtem n
Zdravím
Možná úloha ani není zajímavá (možná ani nemá explicitní řešení) jen si mi jí nedařilo vyřešit tak jak bych chtěl, tak jí dávám sem.
Kolik existuje k-ciferných čísel, neobsahující nulu (žádná z cifer v deakadickém zápisu není nulové) aby ciferný součet byl n?
(například kolik existuje trojciferných čísel s ciferným součtem 10, aby v dek. zápisu nebylo číslo nula, tedy například číslo 703 nepočítáme)
Mě se podařilo odvodit pouze rekurentní vzorec (při pevně zvoleném n) a ani nevím jestli je správný.
Offline
#2 26. 05. 2014 16:28
Re: Počet k-místých čísel s ciferným součtem n
Ahoj ↑ Brzls:,
Mas pravdu, ide o bezne cvicenie.
Na jeho riesenie mozes napisat vsetki moznosti ako napisat 10 ako sucet nenulovych cisiel, a z kazdeho suctu vyvodit kolko da moznych cisiel.
10=1+1+8, to da 3 cisla: 118, 181, 811
10=1+2+7, to da 6 cisiel:...
Pokracuj! Pozor, treba byt systematicky aby si na nic ne zabudol.
Napis tu celkom podrobne tvoje riesenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 26. 05. 2014 16:32 — Editoval Bati (26. 05. 2014 16:32)
Re: Počet k-místých čísel s ciferným součtem n
Ahoj ↑ Brzls:,
znáš vytvořující funkce? Něco je i tady http://en.wikipedia.org/wiki/Generating … plications . Vím, že podobné a obecnější úlohy se tím daly snadno řešit. Souviselo to nějak tak, že cifra  odpovídala členu
odpovídala členu 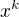 , ale už je to dávno a nepamatuju si, jak se to přesně dělalo.
, ale už je to dávno a nepamatuju si, jak se to přesně dělalo.
Offline
#4 26. 05. 2014 17:28
Re: Počet k-místých čísel s ciferným součtem n
Ahoj ↑ Bati:,
Ta vytvorujuc funkcia co hladas je v tomto pripade  .... z ktorej urcenie koeficientu pred
.... z ktorej urcenie koeficientu pred 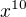 da odpoved na polozene cvicenie.
da odpoved na polozene cvicenie.
No mne sa zda, ze to nie je najlepsi pristup na urovni strednej skoly.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 26. 05. 2014 20:16
Re: Počet k-místých čísel s ciferným součtem n
Ahoj ↑ vanok:,
díky za doplnění, to je ona. Pravda je, že korektní zdůvodnění proč lze použít vytv. posl. je mimo střední školu. Jejich aplikace jsou ale hezké a jednoduché a z vlastní zkušenosti vím, že leccos z toho se dá pochopit na střední.
Offline
#6 26. 05. 2014 20:32 — Editoval Brzls (26. 05. 2014 20:33)
Re: Počet k-místých čísel s ciferným součtem n
↑ vanok:
Zdravím
Kdybych měl takto vypisovat všechny možnosti tak dostanu
118
127
136
145
226
235
244
334
varianty, ve kterých se každá číslice obsahuje právě jednou dají 6 čísel, kde dvě tak 3 čísla
Když to sečtu, tak dostanu 36.
Takhle pro malá čísla je to jasné, jenže takovýto postup se mi nedaří zobecnit na libovolná k a n, resp nedaří se mi najít výraz f(k,n) který by obecně řešil tuto úlohu, potřeboval bych více popíchnout.
Já to původně řešil tak, že takových čísel která začínají 1 je osm, začínající na 2, sedm ... začínající na 8 je 1. Celkový počet hledaných čísel je tedy 8+7+6+...+2+1.
To se dá zobecnit (k=3) na libovolné n jakožto 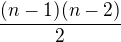 (součet aritmetické řady)
(součet aritmetické řady)
Tím se řeší problém pro k=3
Pro k=4 když si zvolíme první číslici, tak se nám redukuje problém na stejný jako pro k=3.
Například kdybych tentokrát chtěl čtyřciferná čísla s ciferným součtem deset:
první cifra 1: Hledám všechna trojciferná čísla s cif. součtem 9
první cifra 2: Hledám všechna trojciferná čísla s cif. součtem 8
...
první cifra 7: hledám všechna trojciferná čísla s cif. součtem 3
(následně bych tyto dílčí výsledky posčítal)
Když to napíšu v obecném tvaru, tak vyřeším problém i pro k=4 a n libovolné. Takhle můžu postupovat i pro k=5 atd. atd. Jenže nedaří se mi to shrnout do jednoho zápisu pro k libovolné, a i kdyby jo, tak by to byl dost hnusný výraz. Je tato cesta správná?
Nebo jak to co nejelegantněji řešit obecně a dostat výsledek v co nejjednoduším tvaru? Pořád mi to nějak nedochází...
↑ Bati:
Generující funkce jsou opravdu mimo mé rozhledy :)
Offline
#7 26. 05. 2014 20:44
Re: Počet k-místých čísel s ciferným součtem n
To mas pravdu, ze takato metoda je zdlhava. Ak sa najde nejaka relacia typu ako pises, moze sa to zjednodusit.
Ak dokazes pouzit tu generacnu funkciu tak mas vysledky pomerne jenoducho.( ale skoda, ze to presahuje strednu skolu)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 26. 05. 2014 20:46
Re: Počet k-místých čísel s ciferným součtem n
↑ Bati:
Ano uplne suhlasim, mozno by bolo zaujimave napisat nieco jednoduche o tom pre stredoskolakov.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 26. 05. 2014 21:15
Re: Počet k-místých čísel s ciferným součtem n
↑ vanok:
Bohužel na to nemám momentálně čas, zde lze aspoň najít velmi stručný úvod na úrovni střední školy. Mnohem zajímavější než tento článek je učebnice, na kterou se odkazuje a kterou bych zde rozhodně doporučil: Kapitoly z diskrétní matematiky. Tato kniha pokrývá poměrně velké množství zajímavých témat, včetně vytv. fcí, a zároveň k jejímu čtení postačí SŠ znalosti, neboť je psána vlastně jako úvod do VŠ matematiky.
Offline
#10 26. 05. 2014 23:34
Re: Počet k-místých čísel s ciferným součtem n
↑ Bati:,
Ano to moze byt dobry uvod.
Inac aj tu sa pisalo o generacnych funkciach:
http://forum.matweb.cz/viewtopic.php?id=74654
Iste by to mohol pochopit aj motivovany stredoskolak.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 27. 05. 2014 13:58
Re: Počet k-místých čísel s ciferným součtem n
↑ vanok:
Což ten samotný pojem generující funkce mi je jasný a ten příklad z odkazu taky není zrovna dvakrát složitý, ale mě prostě stejně nějak nedochází, jak se to dá použít v tomto příkladě.
Co je tou posloupností, ke které hledám generující funkci? Nebo jak se přišlo například pro to k=3 a n=10, že ta funkce bude zrovna
Mohl byste to nějak rozvést?
Offline
#12 27. 05. 2014 14:40
Re: Počet k-místých čísel s ciferným součtem n
↑ Brzls:,
Generacna funkcia sa nelimituje na pripad n=10, ale dava odpoved (teoreticku) pré vsetki n.
Tu napr  , aby si pochopil ako to funguje ( hladant vysledok sa najde rozvojom pravej strany)... Jeho prve cleny mozes najst aj bez teorie, vdaka rovnosti vysie, stacizacat nasobit
, aby si pochopil ako to funguje ( hladant vysledok sa najde rozvojom pravej strany)... Jeho prve cleny mozes najst aj bez teorie, vdaka rovnosti vysie, stacizacat nasobit 
To ti da zaciatok rozvoja 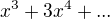
Co da pré n=. 3, mame jedno riesenie.
Pre n= 4, tri.
To nasobenie troch clenov treba robit tak aby si dostal vsetky cleny z 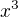 , vpripade n=3 Atd.
, vpripade n=3 Atd.
Pochopitelne ti v rychlosti sa to neda vysvetlit, no hladaj va webe (aj po anglicky, francuzky..) kde mozes najst toho dost vela... a tiez aj pouzi rady moj ho kolegu.
V kazdom pripade ide o zaujimavu teoriu, a iste ti to moze dat chut studovat matematiku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 01. 02. 2020 20:01
Re: Počet k-místých čísel s ciferným součtem n
↑ vanok:
Dobrý den, když jsem četl toto vysvětlení nedokázal jsem přijít proč neroznásobujeme toto 
vždyť můžeme na každé místo vybrat číslice 1-9 a jejich součet musí být 12 (takže se ptáme na koeficient před x na 12( a násobení mocnin o stejném základu je vlastně sčítaní mocnitelů))
Pokud jsem to špatně pochopil, tak prosím o vysvětlení, děkuji.
Offline
#14 01. 02. 2020 21:19 — Editoval vanok (01. 02. 2020 23:03)
Re: Počet k-místých čísel s ciferným součtem n
Ahoj ↑ Pozitron:,
V podstatne mas pravdu, ale pozor akoze ide o zaciatok nekonecneho suctu, tak musis uvazovat tej zatvorke dostatocne vela clenov (ak ti ide o koeficiant napr, pred 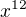 , co znamena, ze hladas ako kolko mas moznosti napisat sucet 12 ).
, co znamena, ze hladas ako kolko mas moznosti napisat sucet 12 ).
Cize v tom pripade potrebujes nast koef. pred 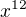 v sucine
v sucine .
.
Ale to je uz iny problem ako ten povodny.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 02. 02. 2020 15:56
Re: Počet k-místých čísel s ciferným součtem n
↑ Pozitron:,
V povodnom cviceni je to tak.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé středoškolské úlohy
- » Počet k-místých čísel s ciferným součtem n

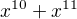 už nemělo patřit, protože se ptáme kolik způsoby můžu ze tří cifer vybrat takové aby jejich součet byl 12?
už nemělo patřit, protože se ptáme kolik způsoby můžu ze tří cifer vybrat takové aby jejich součet byl 12?