Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vzdalenost bodu od oskulační roviny křivky
#2 06. 02. 2020 21:57
- check_drummer

- Příspěvky: 5430
- Reputace: 106
Re: vzdalenost bodu od oskulační roviny křivky
Ahoj, a co ti není jasné?
"Máte úhel beta." "No to nemám."
Offline
#3 07. 02. 2020 09:17 — Editoval surovec (07. 02. 2020 10:45)
Re: vzdalenost bodu od oskulační roviny křivky
↑ Missskkka:
Tak 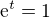 , takže
, takže  .
.
Proto ![kopírovat do textarea $T=\left[ 7;\,0;\,1\right]$](/mathtex/82/82087fbf624ba6688cfcfbd7acb2b312.gif) .
.
Tečný vektor je 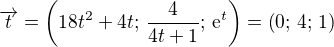 .
.
Vektor druhé derivace je 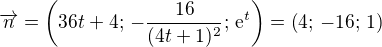 .
.
Normálový vektor hledané roviny je 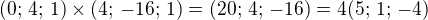 , takže rovina má rovnici
, takže rovina má rovnici 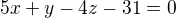 .
.
A vzdálenost bodu od přímky je 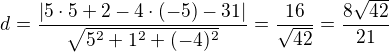 .
.
Offline
#4 07. 02. 2020 10:38
Re: vzdalenost bodu od oskulační roviny křivky
↑ surovec:
Hezký den.
Řekl bych, že je ve výpočtu chybka: Rovina 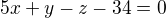 neprochází bodem
neprochází bodem ![kopírovat do textarea $T[ 7;\,0;\,1]$](/mathtex/64/648ce1899aee6c504a73af7cf18c926c.gif) .
.
Myslím, že součin 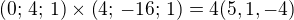 , pak rovnice roviny bude
, pak rovnice roviny bude 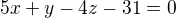 a vzdálenost bodu A od ní bude
a vzdálenost bodu A od ní bude 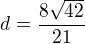
Pokud se tedy nemýlím.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » vzdalenost bodu od oskulační roviny křivky

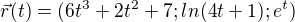 v bode T [?;?;1] dekuji
v bode T [?;?;1] dekuji