Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 02. 2020 13:17
Gonio. rov s parametrem
Ahoj, řeším teď tento příklad a nevím, kde dělám chybu. Budu rád za případné rady
(neumim psat v tom programu na rovnice, snad nevadi, ze to napisu jako text)
cos(odm(a-x^(2)))=1 (2.odmocnina)
mám nají taková a, že bude existovat 8 řešení v mně reálných čísel.
Jednoduše dojdete k
x=(+-) odm(a-4k^(2)pí^(2)).
Nyni sem dosadil do 4k^(2)pí^(2) a jako mnu všech a jsem zvolil interval od k=4 do k=5.
Výsledek je údajně 36pí na druhou až 64 pí na druhou.
pokud jste se v tom alespoň trošku vyznali, budu rád za pomoc :)
Offline
- (téma jako vyřešené označil(a) thorne)

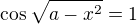


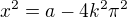

 hodnoty
hodnoty  (ale už ne
(ale už ne  ), tedy
), tedy  ,
, .
.