values on the interval boundaries, so we can look for the roots on the interval and then double the count.
Then, for fixed assuming , for every , there is for
So no matter what, in all points the sign of the value of is determined by expression , which is positive for even and negative for odd and it therefore alternates running through those points.
By intermediate value theorem, has at least real zeros inside the interval .
On the other hand, can be transformed into using transformation
where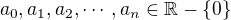 
and 
Then number of real roots of 
in 
![$\cos{(mx)} = \cos{[m(2\pi - x)]}$](/mathtex/7a/7ae16a40a3a3a564d277d76c5f203282.gif "kopírovat do textarea")
for ![$x\in [0,\pi]$](/mathtex/96/96c58ab913f49e0415f17388d6692778.gif "kopírovat do textarea")
and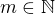 
with nonzero![$[0,\pi]$](/mathtex/13/1337ed550e0d119c374eaa7a1ed6fc47.gif "kopírovat do textarea")
and then double the count.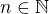 
assuming 
, for every 
, there is for 
the sign of the value of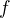 
is determined by expression 
,
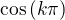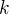and negative for odd 
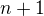points.
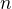real zeros inside the interval 
can be transformed into 
using transformation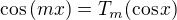
on each term , where 
is 
.
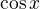is injective function.
.
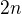real roots on the interval ![$[0,2\pi]$](/mathtex/15/15c80fb5b47715783a5fa5e1aeed97f1.gif "kopírovat do textarea")
.