Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 21. 02. 2020 10:17
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Binomial sum
Thanks ↑ kerajs:
Can u please explain me
Offline
#5 27. 02. 2020 15:24
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: Binomial sum
Thanks ↑ kerajs:
but i did not understand how you calculate 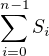 and get the relation
and get the relation 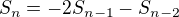
Offline
 Then
Then 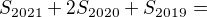



![kopírovat do textarea $
& S_{n}=\sum^{n}_{i=0}(-4)^i \binom{n+i}{2i}=(-1)^n(2n+1)=
\color{blue}{ {n \choose 0} }+\color{black}{\sum_{i=1}^{n-1}(-4)^i {n+i \choose 2i}} + \color{green}{ (-4)^n {2n \choose 2n} }=\\
& =\color{blue}{ {n-1 \choose 0} }+\color{black}{\sum_{i=1}^{n-1}(-4)^i \left[ {n+i -1\choose 2i-1}+{n+i -1\choose 2i}\right]} + \color{green}{ (-4)^n {2n-2 \choose 2n-2} }=\\
& = {n-1 \choose 0}+\sum_{i=1}^{n-1}(-4)^i {n+i -1\choose 2i}-4\left[ \sum_{i=1}^{n-1}(-4)^{i-1} {n+i -1\choose 2i-1}+(-4)^{n-1} {2n-2 \choose 2n-2} \right]=\\
& =S_{n-1}-4 \left[ \sum_{i=1}^{n-1}(-4)^{i-1} \left[ {n+i -2\choose 2i-2}+ {n+i -2\choose 2i-1}\right] +(-4)^{n-1} {2n-2 \choose 2n-2} \right]=\\
& =S_{n-1}-4 \left[S_{n-1}+ \sum_{i=1}^{n-1}(-4)^{i-1} {n+i -2\choose 2i-1}\right]=\\
& =S_{n-1}-4 \left[S_{n-1}+ \sum_{i=1}^{n-2}(-4)^{i-1} {n+i -2\choose 2i-1} + (-4)^{n-2}{2n -3\choose 2n-3}\right]=\\
& =S_{n-1}-4 \left[S_{n-1}+ \sum_{i=1}^{n-2}(-4)^{i-1} \left[{n+i -3\choose 2i-2}+{n+i -3\choose 2i-1} \right] + (-4)^{n-2}{2n -4\choose 2n-4}\right]=\\
& =S_{n-1}-4 \left[S_{n-1}+S_{n-2}+ \sum_{i=1}^{n-2}(-4)^{i-1} {n+i -3\choose 2i-1}\right]=\\
& =S_{n-1}-4 \left[S_{n-1}+S_{n-2}+ \sum_{i=1}^{n-3}(-4)^{i-1} {n+i -3\choose 2i-1}+(-4)^{n-3}{2n -5\choose 2n-5}\right]=\\
& =S_{n-1}-4 \left[S_{n-1}+S_{n-2}+ \sum_{i=1}^{n-3}(-4)^{i-1} \left[{n+i -4\choose 2i-2}+{n+i -4\choose 2i-1} \right] + (-4)^{n-3}{2n -6\choose 2n-6}\right]=\\
& =S_{n-1}-4 \left[S_{n-1}+S_{n-2}+S_{n-3}+ \sum_{i=1}^{n-3}(-4)^{i-1} {n+i -4\choose 2i-1}\right]=\\
& =....=\\
& =S_{n-1}-4 \left[S_{n-1}+S_{n-2}+S_{n-3}+...+S_2+ {2\choose 1} +(-4){3\choose 3} \right]=\\
& =S_{n-1}-4 \left[S_{n-1}+S_{n-2}+S_{n-3}+...+S_2+ {1\choose 0}+ {1\choose 1} +(-4){2\choose 2} \right]=\\
& =S_{n-1}-4 \left[S_{n-1}+S_{n-2}+S_{n-3}+...+S_2+S_1 + {1\choose 1} \right]=\\
& =S_{n-1}-4 \left[S_{n-1}+S_{n-2}+S_{n-3}+...+S_2+S_1 + {0\choose 0} \right]=\\
& =S_{n-1}-4 \left[S_{n-1}+S_{n-2}+S_{n-3}+...+S_2+S_1 + S_0 \right]=\\
&= S_{n-1}-4\sum_{i=0}^{n-1}S_i
$](/mathtex/a3/a3c8febe039c101c95457a3da9e6b1a3.gif)

