Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 02. 2020 20:17 — Editoval vanok (25. 02. 2020 19:29)
Generatory pre SL2(Z)
Pozdravujem,
Tu najdete jedno cvicenie ako urcit jeden system generatorov pre  .
.
Kde  oznacuje grupu matic 2x2 z celymi koeficientami determinantu 1.
oznacuje grupu matic 2x2 z celymi koeficientami determinantu 1.
Najprv oznacme
 ,
, ,
, ,
, ,
,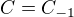 .
.
Dokaz sa da urobit na tri etapy
a) Vypocitajte 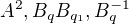 .
.
Urcite  vdaka
vdaka  a
a 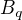 .
.
Urcite rady matic 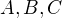 .
.
b)Pre  existuje
existuje 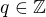 take, ze
take, ze  , take, ze
, take, ze  .
.
Vdaka tomu, dokazte, ze existuje matica  taka, ze,
taka, ze, . (
. ( dostaneme ako sucin matic
dostaneme ako sucin matic  ).
).
A teraz dokazte, ze
c)  je generovana z
je generovana z  a
a  . A tiez aj z
. A tiez aj z  a
a .
.
Poznamka.
Toto cvicenie sa najde v peknej knihe: Nadin, Quitté Algorithmique algébrique.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 20. 02. 2020 05:47
Re: Generatory pre SL2(Z)
Ahoj ↑ Pomeranc:,
Ano.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 21. 02. 2020 09:17
Re: Generatory pre SL2(Z)
Pre tych, co maju problem z #2, staci konstatovat, ze matica  ,
,
ma inverznu maticu  ...
...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 22. 02. 2020 23:11 — Editoval vanok (25. 02. 2020 19:30)
Re: Generatory pre SL2(Z)
Aby ste mohli overit vase riesenie pridavam este toto.
a)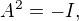 ,
, 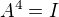 ,
, 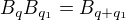 ,
, 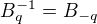 ,
,  ,
, 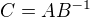 ,
, 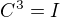 ,
, 
(Iste tiez vidite, ze rad B nie je konecny).
b) tu staci urobit suvis z euklidovskym delenim, ( myslite na delenie cisla a cislom b: co sa moze napisat aj takto kde
kde  ... )
... )
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

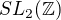 tvoří grupu :) ?
tvoří grupu :) ?