Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 03. 2020 13:41 — Editoval thorne (03. 03. 2020 14:50)
gonio vzorec
Výraz
lze zapsat takto:
přičemž K, fí nezávisí na x. Urči K, fí.
fí i K mám, ale nejsem schopen určit takovou maličkost: kdy je K kladné, a kdy záporné v závislosti na A,B


díky
EDIT: 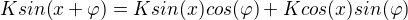
z toho urcim A,B

obě rovnice dám na druhou a sečtu. Pak získám 
Dával jsem to celé na druhou a pak odmocňoval, tak proto se ptám
Offline
- (téma jako vyřešené označil(a) thorne)
#5 03. 03. 2020 14:32
Re: gonio vzorec
↑ surovec:
Já taky né, podle mě je K vždycky kladné...řeší se to volbou toho úhlu
Online
#6 03. 03. 2020 14:43
Re: gonio vzorec
↑ MichalAld:
az se dostanu dom, tak to rozepisu, ale mozna mate pravdu, co ja vim :)
Offline
#10 03. 03. 2020 16:22
Re: gonio vzorec
↑ MichalAld:
Thorne chtěl totiž napsat  , což bylo zřejmé z výpočtu. Proto se ptal, kdy je
, což bylo zřejmé z výpočtu. Proto se ptal, kdy je  kladné a kdy záporné.
kladné a kdy záporné.
Online

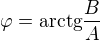 , potom
, potom  .
. , potom staci vzit vzdy
, potom staci vzit vzdy 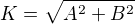
 a
a  , potom bude vždy nezáporné. Jediný prípad ktorý môžeš osobitne ošetriť je
, potom bude vždy nezáporné. Jediný prípad ktorý môžeš osobitne ošetriť je 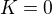 .
.