Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Nerovnost svatého Dalibora (TOTO TÉMA JE VYŘEŠENÉ)
#1 04. 06. 2009 01:48 — Editoval Kondr (04. 06. 2009 11:11)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Nerovnost svatého Dalibora
Nechť x,y,z jsou kladná reálná čísla splňující 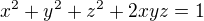 .
.
Najděte nejmenší M takové, že je splněna nerovnost 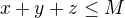 .
.
Autorem úlohy je pravděpodobně docent Švrček z UPOLu (přinejmenším já ji znám od něj).
HINT: Pokud se snažíte dokázat, že minimální takové M je
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#2 04. 06. 2009 04:18 — Editoval xxsawer (04. 06. 2009 12:51)
Re: Nerovnost svatého Dalibora
Offline
#3 04. 06. 2009 08:34
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Nerovnost svatého Dalibora
↑ Kondr:
Asi jsi chtěl napsat \sqrt[3]...
Jinak došel jsem dosti hodně nestandardním postupem k výsledku jako ↑ xxsawer:, takže to zkusím ještě jinak.
Offline
#4 04. 06. 2009 11:11
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Nerovnost svatého Dalibora
↑ xxsawer:↑ halogan:Že já vždycky to zadání zajímavé úlohy popletu ... jistě, máte oba pravdu.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 04. 06. 2009 11:15
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Nerovnost svatého Dalibora
↑ Kondr:
Pěkné.
↑ xxsawer:
Kdyžak příště použij bb element hide. [ hide ] [ / hide ] bez mezer.
Ať si ostatní také užijí.
Offline
#6 04. 06. 2009 11:24 — Editoval Marian (04. 06. 2009 11:29)
Re: Nerovnost svatého Dalibora
Už jsem se dneska ráno té odmocniny začínal bát, protože jsem našel racionální hodnotu čísla M.
↑ xxsawer: Důkaz by nebyl?
↑ Kondr: Odkud název "Nerovnost svatého Dalibora"?
Offline
#7 04. 06. 2009 12:16
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Nerovnost svatého Dalibora
↑ Marian: Nazývat zajímavé úlohy jen podle měsíců a ročních období nebude při větším počtu úloh možné, tak jsem se podíval, kdo má dnes svátek ;)
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#8 04. 06. 2009 12:54 — Editoval xxsawer (04. 06. 2009 12:55)
Re: Nerovnost svatého Dalibora
Offline
#9 04. 06. 2009 14:35
#10 04. 06. 2009 16:34
Re: Nerovnost svatého Dalibora
↑ halogan:
Záměnnost proměnných neimplikuje jejich rovnost - tedy skutečně nematematický soud. Jistě najdeš i jiné hodnoty proměnných, které si nejsou současně rovny a přesto splňují vazební podmínku.
Offline
#11 24. 06. 2009 18:33
Re: Nerovnost svatého Dalibora
Jak bych to řešil já:
Offline
#12 24. 06. 2009 22:58
Re: Nerovnost svatého Dalibora
↑ mmmmario:
Řešení nerovnic pomocí derivací bývá obecně označováno jako "nehezké". Existuje u těchto úloh pojem "nice solution", který vyžaduje řešení bez použití diferenciálního počtu. Řešení jsou o mnoho elegantnější a matematicky hlubší. Ale tvou metodu jsem používal také často.
Offline
#13 21. 01. 2010 01:54
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Nerovnost svatého Dalibora (TOTO TÉMA JE VYŘEŠENÉ)

 , která má dvojnásobný kořen -1 a jednoduchý kořen 1/2. Tedy platí
, která má dvojnásobný kořen -1 a jednoduchý kořen 1/2. Tedy platí

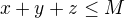 , musí být 3t, tedy 3/2.
, musí být 3t, tedy 3/2. na objektu (množimě, za podmínky, nebo jak se to jmenuje)
na objektu (množimě, za podmínky, nebo jak se to jmenuje) 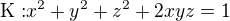 , z toho mi vyšel podezřelý bod
, z toho mi vyšel podezřelý bod 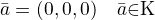 . Dále bych určil body podezřelé z vázaných extrémů vzhledem k
. Dále bych určil body podezřelé z vázaných extrémů vzhledem k  (hranice K, to jsem ale mohl udělat už na začátku (asi, protože ten objekt je přímka?)). Tam to ale vázne na vyřešení soustavy rovnic:
(hranice K, to jsem ale mohl udělat už na začátku (asi, protože ten objekt je přímka?)). Tam to ale vázne na vyřešení soustavy rovnic: ,
, 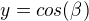 ,
, 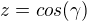 , zadaná podmínka nám dává, že
, zadaná podmínka nám dává, že 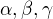 jsou úhly v ostroúhlém trojúhelníku a z Jensena je součet x+y+z maximální pro
jsou úhly v ostroúhlém trojúhelníku a z Jensena je součet x+y+z maximální pro 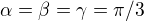 .
.