Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 03. 2020 17:13
Parciální derivace - odvození vztahu
Dobrý den,
prosím o nakopnutí k tomuto příkladu: Dokažte, že ze stavové rovnice ideálního plynu 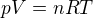 vyplývá:
vyplývá: 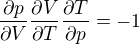 . Vyjádřil jsem si pro každou proměnnou funkční vztah a zderivoval, ovšem to mi nevychází.Nebo se zde jedná o smísené derivace?
. Vyjádřil jsem si pro každou proměnnou funkční vztah a zderivoval, ovšem to mi nevychází.Nebo se zde jedná o smísené derivace?
Offline
#2 09. 03. 2020 17:43 — Editoval Ferdish (09. 03. 2020 17:44)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Parciální derivace - odvození vztahu
↑ Matytus:
Postupoval si správne, akurát po vzájomnom vynásobení výrazov pre parciálne derivácie a vykrátení veličín sa znova pozri na pôvodnú rovnicu :-)
Offline
#3 09. 03. 2020 18:19
Re: Parciální derivace - odvození vztahu
↑ Ferdish:
Děkuji,
když mám tedy pro  ,
, 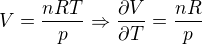 ,
, 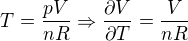 ?Když vynásobím, moc se mi nekrátí.Dělám chybu ve vyjádření?
?Když vynásobím, moc se mi nekrátí.Dělám chybu ve vyjádření?
Offline
#4 09. 03. 2020 19:05
Re: Parciální derivace - odvození vztahu
↑ Matytus:
Nerobis nic zle (az na preklep za sipkou pri "T", ale to je drobnost). Skus urobit to, co ti napisal vyssie Ferdish. Popripade , ak to mam napisat inak, zamysli sa, comu sa rovna: 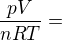 respektive
respektive 
Offline
#5 09. 03. 2020 19:25 — Editoval Matytus (09. 03. 2020 19:26)
Re: Parciální derivace - odvození vztahu
↑ Kenniicek:
Po vynásobení mi vyšlo 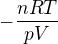 , tudíž záporná převrácena hodnota výrazu
, tudíž záporná převrácena hodnota výrazu  .
.
Offline
#6 09. 03. 2020 20:18
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Parciální derivace - odvození vztahu
↑ Matytus:
A čo tak do výrazu 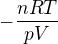 skúsiť dosadiť za čitateľa alebo menovateľa práve z rovnice
skúsiť dosadiť za čitateľa alebo menovateľa práve z rovnice 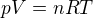 , hm?
, hm?
Offline
#9 10. 03. 2020 15:45
Re: Parciální derivace - odvození vztahu
↑ Ferdish:
Normálně jsem krátil, jako by to byly zlomky.
Offline
#10 10. 03. 2020 16:09 — Editoval Ferdish (10. 03. 2020 16:15)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Parciální derivace - odvození vztahu
↑ ježek:
To ale nie sú zlomky, ale parciálne derivácie.
Použitie Leibnizovho značenia pre deriváciu funkcie  podľa premennej
podľa premennej  ako
ako 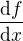 (eventuálne parciálnej derivácie ako
(eventuálne parciálnej derivácie ako 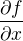 ) k tomu zvádza, ale nie je to matematicky korektný postup.
) k tomu zvádza, ale nie je to matematicky korektný postup.
Rovnakou úvahou (krátením a ponechaním jedinej premennej) by si tiež došiel k záveru 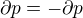 alebo
alebo 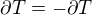 .
.
Viac by sa k tomu vedel vyjadriť kolega MichalAld.
Offline
#12 10. 03. 2020 17:50
Re: Parciální derivace - odvození vztahu
Ferdish napsal(a):
Viac by sa k tomu vedel vyjadriť kolega MichalAld.
No to si nejsem úplně jistý, tady ta termodynamika zrovna nepatří mezi moje nejsilnější stránky.
Ty úpravy, co s tak velkou oblibou dělají fyzikové, tedy ve stylu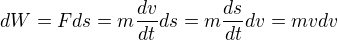
jsou takzvané formální úpravy. Ty členy typu ds či dt nemají samy o sobě žádný přesný matematický význam, nebo jen nějaký extrémně abstraktní. Na druhou stranu, v reálném světě můžeme tyto nekonečně malé elementy nahradit konečně malými elementy, a získat tak nějakou reálnou představu o tom, co vlastně děláme.
Tyhle úpravy by mělo jít vždy zapsat nějakým matematicky korektním způsobem (ale přiznám se, že né vždy se mi to podařilo vymyslet).
Každopádně bychom za tím měli vidět nějakou tu funkci, kterou derivujeme.
U parciálních derivací je to obzvlášť ošidné, protože máme funkci více proměnných.
Tenhle příklad je ovšem nějaký vyumělkovaný ... a nikdy jsem se s ničím takovým v termodynamice nesetkal.
V tomto příkladě jde totiž o 3 různé funkce,
p = p(V, T)
V = V(p, T)
T = T(p, V)
S tímhle se v termodynamice setkáme málokdy, zpravidla si vybereme nějaké dvě proměnné jako nezávislé, a ostatní veličiny vyjadřujeme pomocí těchto funkcí. Běžně se používají jako nezávislé V a T, protože umožňují zkoumat děje "za konstantního objemu" což nám situaci dost zjednoduší. Chemici naproti tomu milují nezávislé proměnné p a T ... protože jim se mnohem lépe dělají experimenty "za konstantního tlaku (atmosférického)", i když to věci po teoretické stránce lehce komplikuje.
Každopádně - tady máme tři funkce, které samozřejmě nejsou úplně nezávislé, protože jde o ideální plyn ... stačí je tedy vyjádřit z toho implicitního tvaru stavové rovnice, poderivovat podle příslušných proměnných a dostaneme: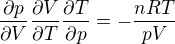
Protože však víme, že platí 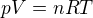 , tedy že platí
, tedy že platí 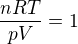 , můžeme to dosadit do té předchozí rovnice a získáme co získáme (že se to rovná -1).
, můžeme to dosadit do té předchozí rovnice a získáme co získáme (že se to rovná -1).
Offline
#13 10. 03. 2020 18:07
Re: Parciální derivace - odvození vztahu
To, že nemůžeme jednotlivé symboly parciálních derivací proti sobě krátit je nejspíš důsledkem toho, že jde o 3 různé funkce. Krátit bychom je mohli v případě, že by šlo o složené funkce, ale to není tento případ.
Kdybychom třeba měli nějakou složenou funkci (ukážu to jen pro funkci jedné proměnné)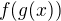
Tak její derivaci vypočítáme jako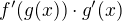
Což by se formálně zapsalo jako: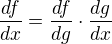
Potom to vypadá, že ta dg proti sobě opravdu můžeme vykrátit.
Ale v tom případě se stavovou rovnicí to tak není ... kdybychom třeba vyjádřili tlak jako funkci objemu a teploty, tedy p = nRT/V, a objem následně také jako funkci teploty, tedy V = V(T), tak bychom nějaké to "krácení" či "rozšiřování" dělat mohli, tedy
Upozorňuji ale, že tohle je nějaká úplně speciální narafičená situace, a ten vztah mezi objemem a teplotou (V=V(T)) musíme zařídit nějak extra, samotý plyn nám ho nezařídí, tam jsou to nezávislé veličiny.
Můžeme si zde ovšem demonstrovat rozdíl mezi symbolem obyčejné a parciální derivace ... protože když používáme tyhle složené funkce typu f(g(x)), případně f(g(x,y),h(x,y)) můžeme pomocí nich rozlišovat, kterou část ze složené funkce máme na mysli.
Offline
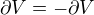 je tam proto, že oba diferenciály jdou k nule?
je tam proto, že oba diferenciály jdou k nule?