Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 03. 2020 17:48 — Editoval NicaNikaNik (16. 03. 2020 18:02)
- NicaNikaNik
- Zelenáč
- Příspěvky: 4
- Reputace: 0
Úloha geometrie v rovině
Hezké odpoledne všem,
Měla bych otázku, teda spíše žádám o pomoc.
Mám úlohu do matematiky a nejsem schopná na to přijít, ikdyž se to zdá jednoduché.
Zadání:
Do čtverce je vepsán čtverec tak, že jeho vrcholy dělí strany původního čtverce v poměru 1:2. Vypočtěte poměr obsahů obou čtverců.
Budu ráda za jakoukoliv pomoc, protože mám v hlavě úplné okno
Offline
- (téma jako vyřešené označil(a) NicaNikaNik)
#2 16. 03. 2020 17:54 — Editoval surovec (16. 03. 2020 17:55)
Re: Úloha geometrie v rovině
↑ NicaNikaNik:
No tak pokud má velkej čtverec stranu délky 
, tak ten vnitřní má dle Pythagorovky kolik? A pak už jen dáš do poměru jejich obsahy a ty áčka se vykrátí...
(A asi nedělí strany trojúhelníku, ale čtverce, ne?)
Offline
#3 16. 03. 2020 18:01
- NicaNikaNik
- Zelenáč
- Příspěvky: 4
- Reputace: 0
Re: Úloha geometrie v rovině
↑ surovec:
Ano ano, přepsala jsem se.
Offline
#4 16. 03. 2020 18:10 Příspěvek uživatele misaH byl skryt uživatelem misaH.
#5 16. 03. 2020 18:11
- misaH
- Příspěvky: 13459
Re: Úloha geometrie v rovině
↑ NicaNikaNik:
Pôvodná strana 3 dieliky, ak je pomer delenia 1: 2
Offline
#6 16. 03. 2020 18:12
- NicaNikaNik
- Zelenáč
- Příspěvky: 4
- Reputace: 0
Re: Úloha geometrie v rovině
↑ misaH:
To, že má původní strana 3 dílky mi bylo jasné, ale já pořád nějak nedokážu dojít na to, jak přijít na délku strany toho vnitřního trojúhelníku
Zní to blbě, matika nikdy nebyl můj obor :/
Offline
#7 16. 03. 2020 18:15 — Editoval surovec (16. 03. 2020 18:16)
Re: Úloha geometrie v rovině
↑ NicaNikaNik:
Pythagorovkou. Jedna odvěsna je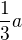 
, druhá 
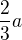a máš spočítat přeponu.
Offline
#8 16. 03. 2020 18:21
- NicaNikaNik
- Zelenáč
- Příspěvky: 4
- Reputace: 0
Re: Úloha geometrie v rovině
↑ surovec:
Panebože, já jsem fakt hloupá!
Děkuju moc.
Offline
#9 16. 03. 2020 18:22
- misaH
- Příspěvky: 13459
Re: Úloha geometrie v rovině
↑ NicaNikaNik:
Základ je urobiť si obrázok, pospájať čo treba
- neverím, že by si sa potom musela pýtať, ten pravouhlý trojuholník je okamžite vidieť a Pytagorova veta priam bije do očí...
Offline
#10 16. 03. 2020 18:55
Re: Úloha geometrie v rovině
↑ NicaNikaNik:
Nevadí, třeba jsi hodná. Nebo hezká. Nebo umíš vařit.
Offline
#12 30. 04. 2024 12:04
Re: Úloha geometrie v rovině
↑ NicaNikaNik:↑ NicaNikaNik:
Můžu se zeptat, kolik ti vyšel ten konečný poměr těch obsahů prosím?
Offline
#14 02. 05. 2024 10:56 — Editoval Honzc (02. 05. 2024 14:34)
#15 02. 05. 2024 14:16
- check_drummer
- Příspěvky: 4894
- Reputace: 105
Re: Úloha geometrie v rovině
A nebo tak, že snadno zjistíme obsah těch 4 shodných pravoúhlých trojúhelníků v rozích toho velkého čtverce a pak už je to jasné.
"Máte úhel beta." "No to nemám."
Online