Matematické Fórum

mateg · 27. 03. 2020 11:00

Dobrý deň, chcem vás poprosiť o pomoc zaujalo ma, že aký postup existuje ak máme nejaký nekonečný súčet, ktorý je konvergetný no lenže dajme tomu, že si zavediem konštantu q a to q sa bude blížiť k nule. Uvediem príklad na lepšie pochopenie majme geometrický rad tvaru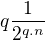
$q\frac{1}{2^{q.n}}$
pričom chceme spraviť jeho nekonečný súčet lenže aj samotné q sa bude blížiť k nule no a keď som to zadal do programu, ktorý jednoduchým cyklom ráta čiastočné súčty radov a ak som zmenšoval q dajme tomu na q=0.00001 a potom som takto sčítal nejakých 100000000 členov tak som došiel k výsledku, ktorý je veľmi blizky
$\frac{1}{ln(2)}=1,442695....$
a keď som skúsil ešte menšie q a ešte väčšie n tak som došiel k výsledku s presnosťou na 5 desatinných miest $1,44269$
a celá moja otázka tkvie v tom, že ako sa s podobnými prípadmi popasovať ak by som nejako cez limity chcel zistil súčty takýchto tu nekonečných radov? vopred vďaka za odpovede

jardofpr · 27. 03. 2020 12:26

ahoj ↑ mateg:

ak tomu rozumiem správne zaujíma ťa ako riešiť úlohu

$\lim_{q\to 0^+} \sum_{n=0}^{\infty}\frac{q}{2^{qn}}$

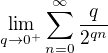
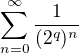mne to pripadá že rad $\sum_{n=0}^{\infty}\frac{1}{(2^{q})^n}$ pre ľubovoľné $q>0$ vieš spočítať ako geometrický,

čo redukuje tvoj problém na jednoduchú limitu

$\lim_{q\to 0^+} \frac{q2^q}{2^q-1} = \lim_{q\to 0^+} \frac{q}{2^q-1} 2^q = \frac{1}{\ln2}\cdot 1$

mateg · 27. 03. 2020 12:52

aha ďakujem za vysvetlenie nie som ešte moc zbehlý v oblasti limit a pod :D

Matematické Fórum

#1 27. 03. 2020 11:00

nekonečný rad jeho súčet a "dvojitá limita"

#2 27. 03. 2020 12:26

Re: nekonečný rad jeho súčet a "dvojitá limita"

#3 27. 03. 2020 12:52

Re: nekonečný rad jeho súčet a "dvojitá limita"

Zápatí