Matematické Fórum

duska · 27. 03. 2020 01:55

Prosímvás, měla bych jednu otázku, jejíž odpověd už dlouho nemůžu nikde najít.
Máme-li diferenciální rovnici: y' = y/x - ve všech bodech až na body ležící na ose x=0, a y' = 5 pro x=0.
Obecné řešení diferenciální rovnice y' = x/t je y = Cx. No mě ale zajímá počáteční řešení, splnující počáteční podmínku y(0) = 0 a proto, abych takovou podmínku vůbec mohla definovat, musím diferenciální rovnici nějak dodefinovat, aby její obor obsahoval bod po kterém požaduji, by ležel na grafu funkce která má být řešením počátečního problému.

Otázky: 1. nevím, jestli takové dodefinování diferenciální rovnici ovlivní její řešení v tom smyslu, že už bude mít jediné řešení: y = 5x, nebo jestli řešení zůstanou, protože všechny funkce y=Cx jsou na intervalu (0, $\infty$ ), nebo (- $\infty$ , 0) řešeními.

2. počáteční úlohu určitě bude splňovat právě funkce y = 5x. Ale pak mě napadlo, že ji možná budou splňovat úplně všechny funkce z řešení, protože jsou v tom bodě spojité a pokud se jenom v jednom bodě limita derivace zleva nerovná limitě derivace zprava, tak to bud nevadí, protože jeden bod nemůže nic zkazit. Je možné, že taková funkce zůstává diferencovatelná? Má počáteční problém nekonečně mnoho řešení, nebo jen jedno?

Děkuji moc... :)

jardofpr · 27. 03. 2020 22:21

ahoj ↑ duska:

môj pohľad

duska napsal(a):
...No mě ale zajímá počáteční řešení, splnující počáteční podmínku y(0) = 0 a proto, abych takovou podmínku vůbec mohla definovat, musím diferenciální rovnici nějak dodefinovat, aby její obor obsahoval bod po kterém požaduji, by ležel na grafu funkce která má být řešením počátečního problému.

Otázky: 1. nevím, jestli takové dodefinování diferenciální rovnici ovlivní její řešení v tom smyslu, že už bude mít jediné řešení: y = 5x, nebo jestli řešení zůstanou, protože všechny funkce y=Cx jsou na intervalu (0, $\infty$ ), nebo (- $\infty$ , 0) řešeními...

Ak je zadanie

$y'=\begin{cases}\frac{y}{x}, \quad & x\in\mathbb{R}-\{0\}\\ 5, \quad & x=0 \end{cases}$ s poč.podmienkou $y(0)=0$

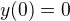
tak derivácia hľadanej funkcie $y$ na celom obore $\mathbb{R}$ je definovaná,
t.j. primárne sa v cvičení očakáva diferencovateľná funkcia $y:\mathbb{R}\to\mathbb{R}$ ako riešenie ak existuje,
nič sa nedodefinováva

duska napsal(a):
...
2. počáteční úlohu určitě bude splňovat právě funkce y = 5x. Ale pak mě napadlo, že ji možná budou splňovat úplně všechny funkce z řešení, protože jsou v tom bodě spojité a pokud se jenom v jednom bodě limita derivace zleva nerovná limitě derivace zprava, tak to bud nevadí, protože jeden bod nemůže nic zkazit. Je možné, že taková funkce zůstává diferencovatelná? Má počáteční problém nekonečně mnoho řešení, nebo jen jedno?

Zdá sa že predpoklady vety o jednoznačnosti riešenia (u nás známa ako Picardova, prípadne Picard-Lindelofova veta)
pre problém $y'=f(x,y(x)), y(x_0)=y_0$ nebudú splnené. Tvoja funkcia $f(x,y) = \frac{y}{x}$ iste

iste nebude rovnomerne Lipschitzovsky spojitá na okolí bodu $x=0$ čo napovedá napr. $\frac{\partial f}{\partial y} = \frac{1}{x}$ ,

takže treba počítať aj s možnosťou nekonečne veľa riešení po aplikovaní počiatočnej podmienky.
(nakoniec pre $f$ samotnú nevieme overiť ani spojitosť v premennej $x$ a teda existenciu riešenia na obore reálnych čísel na začiatku).

V tvojom cvičení po nájdení $y(x) = Cx$ pre $x\in\mathbb{R}-\{0\}$ sa ukazuje že
vieme nájsť potenciálne riešenia diferencovateľné na celom $\mathbb{R}$ ,
ale počiatočná podmienka nevyberie riešenie jednoznačne.
Jednoznačne ho vyberie ale samotné zadanie ktoré udáva hodnotu derivácie $y'=5 (=C)$ v bode $x=0$ .

duska · 28. 03. 2020 00:24 — Editoval duska (28. 03. 2020 00:25)

↑ jardofpr:↑ jardofpr:
Děkuji. Abych lépe vysvětlila situaci. Snažím se zadat počáteční problém tak, aby měl nekonečně mnoho řešení po nesplnění předpokladu ve větě o existenci a jednoznačnosti, kde u lineární diferenciální rovnice stačí spojitost koeficientů k tomu, aby na takovém intervalu existovalo právě jedno řešení.
Zadala bych takový příklad takto:
$x' = x/t$ , $t \in (0,\infty)$ .

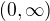Myslíte si, že můžu říct, že tento počáteční problém má řešení, funkce $x = Ct, C \in R$ , kde x je z $(0, \infty)$ , protože dané funkce bodem prochází, ale jako řešení daného počátečního problému, to znaméná, že bychom museli jejich definiční obor omezit pro t z intervalu 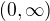$(0, \infty)$ , by už daným bodem neprocházely, protože v něm nejsou řešením dané rovnice. Protože jinak splní podmínky pro řešení: jsou diferencovatelné, spojité, splnují danou diferenciální rovnici. Ale v jedné defiici jsem četla, že bod z počáteční podmínky musí být z oblasti $G$ , což je oblast, v našem pšípadě v R2, ve které je doferenciální rovnice definovaná. Takže celá osa $x$ v $G$ není. Tedy ani počátek, který chci použít v počáteční podmínce.

Děkuji

duska · 28. 03. 2020 10:58 — Editoval duska (28. 03. 2020 11:05)

↑ jardofpr:
Můžu se ještě zeptat, jak jste napsal:

V tvojom cvičení po nájdení $y(x) = Cx$ pre $x\in\mathbb{R}-\{0\}$ sa ukazuje že
vieme nájsť potenciálne riešenia diferencovateľné na celom $\mathbb{R}$ .

Pokud by diferenciální rovnice byla zadána jako: $y' = \frac{y}{x},\quad x > 0$ , budou řešení počáteční podmínky $y(0) = 0$ všechny funkce $y = Cx, x>0$ ? Jsou diferencovatelné... Prostě splnují podmínky řešení, ale nevadí, že jejich graf neprochází bodem z počáteční podmínky? Nebo v tomto případě, kdy se jedná o krajní mez, tak to lze odpustit? A nevadí, že se ptám na bod, který není z $G$ , oblasti, kde diferenciální rovnice, zadaná jako funkce dvou proměnných, není definovaná?

Zní to zajímavě. :) Děkuji za odpověd

jardofpr · 28. 03. 2020 11:46

ahoj

↑ duska:

mne to príde výhradne o tom s akými objektami potrebujem pracovať a teda aké objekty pripustím pre potreby
práce s nimi

keď potrebujem pracovať len s DR pri ktorých žiadam aby počiatočná podmienka bola súčasťou domény
funkcie $f$ (v kontexte o ktorom rozprávam vyššie), nemá potom zmysel aby som skúmal úlohu
s počiatočnou podmienkou ktorá do nej nepatrí a je na jej hranici; o takéto objekty som ochudobnený

keď potrebujem pracovať s takouto úlohou, povolím aj takúto počiatočnú podmienku
za nejakých rozumných podmienok (napr. riešenie si zachová vlastnosti z domény ktoré sú pre mňa dôležité aj na jej hranici)

napríklad v štandardných kurzoch na VŠ sú bežné nároky na $f$ spojitosť pre existenciu riešenia v zmysle
vlastností ktoré toto riešenie spĺňa (Peano existence theorem) a s týmto sa potom pracuje

keď sa chceme zažrať hlbšie môžeme napríklad pripustiť nespojitú $f$ ktorá má nejaké slabšie vlastnosti,
a hľadať riešenie v rozšírenom zmysle, ktoré má zaručenú len v istom zmysle "nižšiu" kvalitu
(Caratheodory existence theorem)

ak chceme ísť ešte ďalej, existujú teoretické výsledky aj pre DR ktoré nepožadujú rád derivácie ako celé číslo
t.j. nemáš len prvú, druhú ... deriváciu ale trebárs poltú atď ..
(differential equations of fractional order)

celé je to o tom kde sa potrebuješ pohybovať a tam potom robíš matematiku

duska · 28. 03. 2020 12:57

↑ jardofpr:
Ted už jsem to pochopila. :) Takže pokud se snažím najít protipříklad, není problém opomenout na to, že počáteční podmínka není z domény G, protože se chci posuout dál a najít něci zajímavého, zachovám-li hlavní vlastnosti řešení - spojitost a diferencovatelnost řešení + řešení vyhovuje rovnici - je podmínka vzít bod z počáteční podmínky z G, pouze maličkost a můžu ji opomenout. Moc děkuji :)

Matematické Fórum

#1 27. 03. 2020 01:55

Diferenciální rovnice, řešení

#2 27. 03. 2020 22:21

Re: Diferenciální rovnice, řešení

duska napsal(a):

duska napsal(a):

#3 28. 03. 2020 00:24 — Editoval duska (28. 03. 2020 00:25)

Re: Diferenciální rovnice, řešení

#4 28. 03. 2020 10:58 — Editoval duska (28. 03. 2020 11:05)

Re: Diferenciální rovnice, řešení

#5 28. 03. 2020 11:46

Re: Diferenciální rovnice, řešení

#6 28. 03. 2020 12:57

Re: Diferenciální rovnice, řešení

Zápatí