Matematické Fórum

↑ Pega:
To je úloha pro ZŠ, jako nakonec většina dnešních "maturitních" úloh.

Udělal jsi zkošku, ale nějak nikde nevidím žádný postup, tak mi není jasné, co zkoušíš. Mně se spíš zdá, že sis vymyslel tři čísla a teď se divíš, že nesplňují zadání. "Polovina těch, kteří mluví anglicky" znamená polovina z lidí, kteří mluví jenom anglicky nebo oběma jazyky současně.

Nakresli si dvě kružice, které se protínají. Označ si třemi písmenky počet lidí, kteří mluví jen anglicky, jen německy a oběma jazyky současně (budou odpovídat plochám na tvém diagramu). Pak pomocí těch písmenek zapiš ty dvě věty ze zadání a mělo by být jasno.

Ze zadání nelze zjistit ani počet pracovníků, ani jaký je poměr anglicky a německy mluvících.
Počítá se jenom se zlomky.
Takže předpokládám, že výsledek musí být stejný pro libovolný počet pracovníků a libovolný poměr anglicky a německy mluvících.
Nebo se mýlím?

Nehnevajte sa, ale toto vôbec nie je triviálna úloha - a ZŠ teda už vôbec nie.


Nakreslila som si úsečku, ktorá reprezentuje počet ľudí, čo hovoria oboma jazykmi.

táto (1.) úsečka predstavuje 1/3 z tých, čo hovoria anglicky - doľava som dorobila ešte dva rovnaké (ako 1.) dieliky tých, čo hovoria iba anglicky

táto (1.) úsečka súčasne predstavuje 1/2 tých, čo hovoria nemecky, takže tí, čo hovoria iba nemecky predstavujú smerom doprava rovnaký 1 dielik

Na obrázku vidno, že pôvodná (1.) úsečka tvorí z celej úsečky (všetci ľudia) jednu štvrtinu.

misaH napsal(a):

Nehnevajte sa, ale toto vôbec nie je triviálna úloha - a ZŠ teda už vôbec nie.

Je to triviální úloha a sama jsi to právě dokázala. Proto také úlohy tohoto typu jsou běžně součástí příjímacích zkoušek na SŠ.

Ani sestavení a řešení rovnic 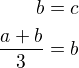mi nepřijde jako nic, co by člověk na ZŠ neměl zvládnout. Ale asi už jsem starý a nemoderní.

Alebo sa da aj využiť teória pravdepodobnosti.
[mathjax]\begin{align}
P{\left(A\cup N\right)}=1 &= P{\left(A\right)}+P{\left(N\right)}-P{\left(A\cap N\right)}\\
P{\left(A|N\right)}=\frac{1}{2} &= \frac{P{\left(A\cap N\right)}}{P{\left(N\right)}}\\
P{\left(N|A\right)}=\frac{1}{3} &= \frac{P{\left(A\cap N\right)}}{P{\left(A\right)}}\end{align}[/mathjax]
Teda
[mathjax]\begin{align}P{\left(N\right)} &= 2P{\left(A\cap N\right)}\\
P{\left(A\right)} &= 3P{\left(A\cap N\right)}
\end{align}
[/mathjax]
Čiže máme
[mathjax]1=3P{\left(A\cap N\right)}+2P{\left(A\cap N\right)}-P{\left(A\cap N\right)}=4P{\left(A\cap N\right)}[/mathjax]
a teda
[mathjax]P{\left(A\cap N\right)}=\frac{1}{4}[/mathjax]