Matematické Fórum

statistika_je_naj

Ahojte, mam za ulohu vytvorit kovariancnu maticu v tomto priklade: https://forum.matweb.cz/viewtopic.php?id=107450

Postupoval som takto:
Vypocital som 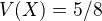$V(X)=5/8$
toiste mi vyslo pre 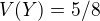$V(Y)=5/8$
uz vypocitany udaj, ktory sme zistili je 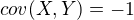$cov(X,Y)= -1$
teda kovariancna matica bude vyzerat:

5/8 - 1
-1 5/8
Mam to spravne prosim vas?

jarrro · 08. 04. 2020 14:53

Ako si dostal 5/8?

statistika_je_naj · 08. 04. 2020 17:07

vychadzal som zo vztahu pre disperziu 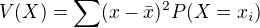$V(X)=\sum_{}^{}(x-\bar{x})^2 P(X=x_i)$
teda najprv som vypocital priemer, ten mi vysiel: 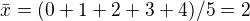$\bar{x}= (0+1+2+3+4)/5=2$
Potom som pocital:
$(0-2)^2 . 1/16 + (1-2)^2 . 4/16 + (2-2)^2 . 6/16 + (3-2)^2 . 4/16 + (4-2)^2 . 1/16 =16/16$
teraz mi to vychadza 1 ... och tak ja neviem ktore je zle a ktore dobre

jarrro · 08. 04. 2020 19:58

↑ statistika_je_naj:áno až na to, že miesto priemeru má byť stredná hodnota. (Tu je to náhodou to isté ale vo všeobecnosti nie)

statistika_je_naj · 08. 04. 2020 20:28

aha, tak ok, dam si na to pozor. Vdaka :)

Matematické Fórum

#1 08. 04. 2020 13:30 — Editoval statistika_je_naj (08. 04. 2020 13:43)

kovariancna matica

#2 08. 04. 2020 14:53

Re: kovariancna matica

#3 08. 04. 2020 17:07

Re: kovariancna matica

#4 08. 04. 2020 19:58

Re: kovariancna matica

#5 08. 04. 2020 20:28

Re: kovariancna matica

Zápatí