Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 04. 2020 20:44 — Editoval statistika_je_naj (08. 04. 2020 20:45)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Diskretny nahodny vektor
Dobry den, mam takuto ulohu a vobec neviem co s nou robit a chcel by som vas poziadat o pomoc:
Pre nahodny vektor 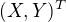 plati:
plati: ![kopírovat do textarea $P[(X,Y)^T = (0,1)^T]=P[(X,Y)^T = (0,0)^T]=P[(X,Y)^T = (1,0)^T]=1/3$](/mathtex/99/994214bb8f733d038414fcb16443be61.gif) . Popiste distribucnu funkciu nahodneho vektora
. Popiste distribucnu funkciu nahodneho vektora 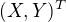 . Urcte
. Urcte ![kopírovat do textarea $P[X=k]$](/mathtex/21/2129096223f0818bc89d15b912a6d120.gif) a
a ![kopírovat do textarea $P[Y=k]$](/mathtex/56/5603d9b6a2afa15f6c5f8ebccdde4e9a.gif) pre
pre 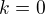 a
a  . Najdite distribucne funkcie nahodnych premennych
. Najdite distribucne funkcie nahodnych premennych  a
a  .
.
Offline
#3 08. 04. 2020 21:22
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: Diskretny nahodny vektor
no ale nejako neviem co s tym dalej
Offline
#4 08. 04. 2020 21:26 — Editoval jarrro (08. 04. 2020 21:26)
Re: Diskretny nahodny vektor
↑ statistika_je_naj:a čo ďalej chceš veď keď vieš pravdepododobnosti tak vieš aj distribučnú fciu
MATH IS THE BEST!!!
Offline
#5 08. 04. 2020 23:34
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: Diskretny nahodny vektor
a vieme pravdepodobnosti? predsa za to  nevieme dosadit ... ci to netreba?
nevieme dosadit ... ci to netreba?
Offline
#6 17. 04. 2020 09:08
Re: Diskretny nahodny vektor
↑ statistika_je_naj:akože nevieme veď k je 0 alebo 1 distribučná fcia bude schodovitá
MATH IS THE BEST!!!
Offline

