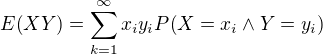Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 07. 04. 2020 18:17 — Editoval jarrro (07. 04. 2020 18:19)
Re: kovariancia
Lebo stredná hodnota je integrál (Lebesguov v pravdepodobnostnom priestore) a pre diskrétne veličiny platí(v základnejších kurzoch sa to považuje za definíciu)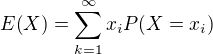
https://en.m.wikipedia.org/wiki/Expected_value
MATH IS THE BEST!!!
Offline
#28 07. 04. 2020 18:44
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
takze cov(X,Y)=-1 a teda su nepriamo zavisle
Offline
#30 07. 04. 2020 18:49
Offline
#31 07. 04. 2020 18:51
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: kovariancia
super, uz tomu rozumiem, velka vdaka.
Este sm sa chcel opytat - moze vynst ajnizsie cislo pri cov(X,Y) ako je -1? Predpokladam ze nie, ide o ukazovatel stopercentnej nepriamej zavislosti? Napokon je to aj logicke, cim viac chlapov - tym menej dievcat. To priamo suvisi.
Offline
#32 09. 04. 2020 11:36
Re: kovariancia
↑ statistika_je_naj:kovariancia môže aj nižšie ako -1 prečo by nemohla? Korelácia je medzi -1 a 1
MATH IS THE BEST!!!
Offline