Matematické Fórum

Marcia24 · 09. 04. 2020 10:28

Dobrý den, co je tady prosím za úpravu? Děkuji
//forum.matweb.cz/upload3/img/2020-04/20850_V%25C3%25BDst%25C5%2599i%25C5%25BEek.PNG

surovec · 09. 04. 2020 11:46

↑ Marcia24:
Tam asi chybí nějaká informace z předchozího textu...

jardofpr · 09. 04. 2020 17:15

ahoj ↑ Marcia24:

nie je to vobec jednoriadkova zalezitost

odvodenie mozes najst napriklad tu, strany 93-94,
ale bude to chciet vratit sa aj k predchadzajucemu textu ku ktoremu sa na tychto stranach autor odkazuje

Chandrasekhar-Introduction to study of stellar structure

laszky · 10. 04. 2020 04:41 — Editoval laszky (10. 04. 2020 12:19)

↑ Marcia24:

Ahoj, transformace 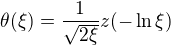$\theta(\xi)=\frac{1}{\sqrt{2\xi}}z(-\ln\xi)$ prevede rovnici na 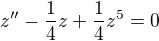$z''-\frac{1}{4}z+\frac{1}{4}z^5=0$ . Prenasobenim 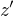$z'$ ziskas

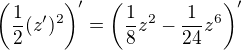$\left(\frac{1}{2}(z')^2\right)' = \left(\frac{1}{8}z^2-\frac{1}{24}z^6\right)'$ , takze $\frac{1}{2}(z')^2 = \frac{1}{8}z^2-\frac{1}{24}z^6 + D$ .

Pro D=0 ziskas 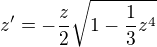$z' = -\frac{z}{2}\sqrt{1-\frac{1}{3}z^4}$ a separaci promennych a integraci vyjde

$z(t)=\sqrt[4]{\frac{12C^2\mathrm{e}^{-2t}}{(1+C^2\mathrm{e}^{-2t})^2}}$ , takze $z(-\ln\xi)=\sqrt[4]{\frac{12C^2\xi^2}{(1+C^2\xi^2)^2}}$ , a proto $\theta(\xi)=\sqrt[4]{\frac{3C^2}{(1+C^2\xi^2)^2}}$ .

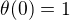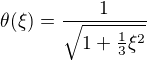Z okrajove podminky $\theta(0)=1$ nakonec vyjde $C^2=\frac{1}{3}$ , a tak $\theta(\xi)=\frac{1}{\sqrt{1+\frac{1}{3}\xi^2}}$ . (Strucny vytah z uvedeneho odkazu)

jardofpr · 10. 04. 2020 08:32

ahoj ↑ laszky:

mas pocit ze by kolegyna nezvladla si toto iste precitat z odkazu ktory som uviedol?
alebo si si potreboval precvicit prepisovanie do latexu?

laszky · 10. 04. 2020 11:04 — Editoval laszky (10. 04. 2020 12:20)

↑ jardofpr:

Ahoj, rad pomuzu. Preji krasne Velikonoce.

Matematické Fórum

#1 09. 04. 2020 10:28

Diferenciální rovnice

#2 09. 04. 2020 10:38 Příspěvek uživatele jarrro byl skryt uživatelem jarrro. Důvod: Omyl

#3 09. 04. 2020 11:46

Re: Diferenciální rovnice

#4 09. 04. 2020 17:15

Re: Diferenciální rovnice

#5 10. 04. 2020 04:41 — Editoval laszky (10. 04. 2020 12:19)

Re: Diferenciální rovnice

#6 10. 04. 2020 08:32

Re: Diferenciální rovnice

#7 10. 04. 2020 11:04 — Editoval laszky (10. 04. 2020 12:20)

Re: Diferenciální rovnice

Zápatí