Matematické Fórum

noidea · 10. 04. 2020 21:30

Zdravím,
potřebovala bych poradit s úkolem do statistiky, se kterým už se nějakou dobu trápím. Většinou jsem schopná spočítat příklady, ale tady ty "teoretičtější" věci jsou trochu mimo mě, tak bych to chtěla konečně pochopit. :-)

Víme tedy, že jde o náhodnou veličinu X s rovnoměrným rozdělením na intervalu (-1,1). Dále víme, že náhodná veličina Y je dána předpisem 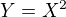$Y = X^{2}$ .

Už jsem vypočítala, že střední hodnota (EX) bude 0 a rozptyl X (var X) je 1/3.

Tak a teď už k úkolu - má více částí.

1) Určit střední hodnotu a rozptyl Y, a to jednak ze vztahu 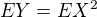$EY = EX^{2}$ , tak i přímo z definice střední hodnoty. Platí také $var Y = EY^{2} - (EY)^{2}$ .

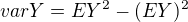2) Určit kovarianci a korelační koeficient X, Y. Platí: 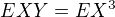$EXY = EX^{3}$ a $cov(X,Y) = EXY - EX * EY$ .

3) Určit, zda jsou závislé a proč. Tady bych řekla, že jsou, ale nedokážu to vysvětlit, tudíž je mi to k ničemu, že.

Děkuji všem za ochotu a za pomoc.

nejsem_tonda

↑ noidea:
Mozna ti k vyreseni ulohy brani to, ze nemas uplne ujasneno, co znamena pocitat stredni hodnotu. (Jenom odhaduju.)
Predpokladam, ze vis, ze kdyz oznacim hustotu veliciny X, tak potom

V nasi uloze je f(x) nulova mimo interval (-1; 1) a rovna 1/2 na intervalu (-1; 1).
Co uz mozna nevis, je to, ze pocitat stredni hodnotu treba veliciny znamena pocitat integral

Jinymi slovy, trochu nepresne:
* z veliciny udelam funkci $x^5-3x^2$
* kdyz pred velicinu napisu , je to totez jako kolem te funkce nakreslit integral

Tohle by mohlo pomoct. Napriklad spocitat , coz je zkraceny zapis E(XY), je tedy totez jako pocitat , tedy

V nasem pripade se integral zjednodusi na

Zkusis to ted znovu?

nejsem_tonda · 11. 04. 2020 00:00

↑ noidea:
Zapomnel jsem na tu (ne)zavislost. Ono je tady intuitivne naprosto jasne, ze zavisle jsou (protoze preci Y je dane predpisem pomoci X, takze je na nem "naprosto zavisle"). Kdybych to chtel zduvodnit presneji, spocitam treba pravdepodobnost
(ty zlomky jsem mohl volit mnoha ruznymi zpusoby)
a porovnam se soucinem pravdepodobnosti

Zvladnes to dokoncit?

noidea · 11. 04. 2020 11:18

Díky moc za pomoc!

To EXY, EY, atd. jsem už nějak dopočítala, akorát jsem zjistila, že k tomu potřebuju ještě dopočítat výběrové protějšky (k té kovariaci a koleračnímu koeficientu) - to už vůbec netuším, jak na to dojít.
Jestli se můžu zeptat, odkud víme, že f(x) je na intervalu (-1,1) rovna 1/2? A mimo ten interval 0?

Ještě se přiznám, že u té závislosti nemám tušení jak spočítat pravděpodobnost toho průniku. Pravděpodobnost pro X>1/2 mi vyšla 3/4 a pro Y<1/9 mi vyšla 1/6.

Omlouvám se za takové základní otázky - většinou se tyhlety věci učím na přednáškách/cvikách (potřebuju to "vidět", abych to pochopila). Teď tím, že hodiny nejsou, tak mám k dispozici akorát teorii a když mi to nikdo nepředvede, tak je to pro mě těžké pochopit.

nejsem_tonda

↑ noidea:
Nevim, co se nazyva vyberovym protejskem. Mne prijde, ze pro vypocet kovariance / korelacniho koeficientu uz vsechno znas. Pro kovarianci jsou to tri cisla: EXY, EX, EY (tedy ) a korelacni koeficient je pouze "znormovana kovariance" - kovarianci vydelis cisly a , ktere uz taky mas spocitane.

Tu hustotu vime z teto vety zadani

jde o náhodnou veličinu X s rovnoměrným rozdělením na intervalu (-1,1)

Rovnomernost rika, ze zadne hodnoty v intervalu (-1,1) nejsou pravdepodobnejsi nez nejake jine. Jinymi slovy to rika, ze hustota je vodorovna usecka.
Mimo interval (-1, 1) se velicina X podle zadani nemuze dostat, proto tam je nulova. Na intervalu (-1, 1) je ta vodorovna usecka tak vysoko, aby jev mel pravdepodobnost 1, tedy ma platit
, proto pro

Pravdepodobnost, ze X>1/2 je 1/4, protoze me vlastne zajima, jak velkou cast z intervalu (-1, 1) tvori interval (1/2, 1).
Pravdepodobnost, ze Y<1/9 je stejna jako pravdepodobnost, ze X^2<1/9, takze tady me zajima, jak velkou cast z intevralu (-1, 1) tvori interval (-1/3, 1/3).
Pravdepodobnost toho pruniku se prelozi jako pravdepodobnost, ze X>1/2 a zaroven X^2<1/9. Tedy zajima nas, kdy je velicina X v intervalu (1/2, 1) a zaroven v intervalu (-1/3, 1/3).

noidea · 11. 04. 2020 13:11

Skvělé, díky za vysvětlení! Už mi to všechno začíná zapadat do sebe. :-)

K těm výběrovým protějškům jsem našla tohle - https://iastat.vse.cz/regrese/Korelace2.htm , tak s tím už si snad nějak poradím sama.

nejsem_tonda · 11. 04. 2020 13:39

↑ noidea:
Aha, ok, to se tyka situace, kdy nevim, jak je presne rozlozena hustota veliciny X a tu hustotu se snazim odhadnout z toho, jake hodnoty veliciny X jsem nameril.

Muzes si to predstavit tak, ze bych ti dal hraci kostku, rekl bych ti, ze je zamerne "cinkla" (nejaka cisla padaji casteji nez jina), ale nerekl bych ti nic vic. Potom jedine, co mas moznost udelat, je, ze s ni treba 100krat hodis a zaznamenas si, co ti padalo. V takovych pripadech se pocitaji ty vyberove veci.

Matematické Fórum

#1 10. 04. 2020 21:30

Statistika, náhodná veličina a teoretické odvození

#2 10. 04. 2020 23:16 — Editoval nejsem_tonda (10. 04. 2020 23:22)

Re: Statistika, náhodná veličina a teoretické odvození

#3 11. 04. 2020 00:00

Re: Statistika, náhodná veličina a teoretické odvození

#4 11. 04. 2020 11:18

Re: Statistika, náhodná veličina a teoretické odvození

#5 11. 04. 2020 12:42 — Editoval nejsem_tonda (11. 04. 2020 12:44)

Re: Statistika, náhodná veličina a teoretické odvození

#6 11. 04. 2020 13:11

Re: Statistika, náhodná veličina a teoretické odvození

#7 11. 04. 2020 13:39

Re: Statistika, náhodná veličina a teoretické odvození

Zápatí