Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 04. 2020 13:59
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
stredna hodnota nahodneho vektora
Dobry den. nasiel som definiciu strednej hodnoty nahodneho vektora a priznam sa , ze jej az tak nerozumiem. Pise sa tam, ze je to toto:
Pre nahodny (dvojrozmerny) vektor 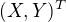 ktory nadobuda hodnoty
ktory nadobuda hodnoty 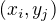 kde
kde 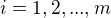 a
a 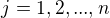 s kladnymi pravdepodobnostami
s kladnymi pravdepodobnostami 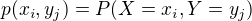 je stredna hodnota premennej
je stredna hodnota premennej  rovna
rovna 
Ako si to mam predstavit, ze co je vlastne ta stredna hodnota? Ako by sa to pocitalo pre nejaky konkretny priklad, pre nejake konkretne hodnoty 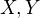 ?
?
Offline
#2 13. 04. 2020 10:34
Re: stredna hodnota nahodneho vektora
tu je v hre viac veci, mas tam nahodny vektor (X,Y), mas tam nahodnu premennu Z ktora sa vypocita ako Z=h(X,Y) a jej strednu hodnotu.
Kym sa pozrieme na jednotlive kroky, napis ci ci vies aka je definicia strednej hodnoty ak mas iba jednu nahodnu premennu X; t.j. ako sa vypocita E(X) ... a ci vies co znamena
Offline
#3 15. 04. 2020 15:12 — Editoval statistika_je_naj (15. 04. 2020 15:13)
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: stredna hodnota nahodneho vektora
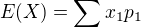 a to znamena ze vynasobim ten jav
a to znamena ze vynasobim ten jav  s pravdepodobnostou ze nastane teda
s pravdepodobnostou ze nastane teda  .
.
Offline
