Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 04. 2020 12:43
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
studentovo rozdelenie
Ahojte mam takuto ulohu a chcel by som si overit ci to pocitam spravne:
Vykonali sme 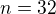 analyz na overenie koncentracie chemickej latky v roztoku. Predpokladajme, ze koncentracia ma normalne rozdelenie
analyz na overenie koncentracie chemickej latky v roztoku. Predpokladajme, ze koncentracia ma normalne rozdelenie 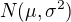 , kde
, kde 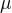 je neznamy parameter a
je neznamy parameter a 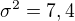 . Vysledky analyzy su v tabulke rozdelenia pocetnosti:
. Vysledky analyzy su v tabulke rozdelenia pocetnosti: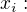 9, 11,12,14,15,16,17,18,20,21
9, 11,12,14,15,16,17,18,20,21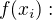 1,2,3,4,7,5,4,3,2,1
1,2,3,4,7,5,4,3,2,1
Urcte 99 %- tny dvojstranny interval spolahlivosti pre neznamu strednu hodnotu 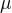 .
.
Moje riesenie:
Vypocital som najprv 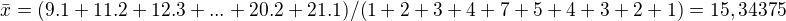
potom som vypocital: ![kopírovat do textarea $s^2 = 1/n-1 \sum_{i=1}^{n} (x_i -\bar{x})^2 = 1/32 [(9-15,34375)^2 + (11-15,34375)^2 +... +(21-15,34375)^2 ]=4,39094$](/mathtex/9d/9d5e8a868edacede2d6fcbdce367311c.gif)
teda plati: 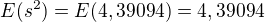 a odtial mame:
a odtial mame: 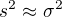 teda
teda 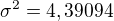 a odtial dostaneme
a odtial dostaneme 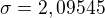
ten interval 99 % spolahlivosti som urcil takto: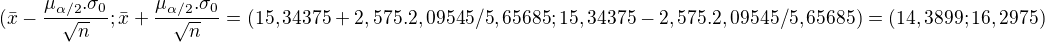
Teda 99 % interval je 
Offline
#2 20. 04. 2020 19:57
Re: studentovo rozdelenie
Vidím, že nikdo neodpovídá, tak zkusím já, přestože se to učím na dálku taky tento semestr Postup je správně, jen hodnota toho kvantilu studentova rozdělení pro 32 analýz (takže 31 stupňů volnosti) je 2,774 (tabulka třeba tady: http://albertskblog.blogspot.com/2010/0 … table.html, ty to počítáš s 2,575, což je hodnota pro nekonečně mnoho stupňů volnosti).
Offline
#3 22. 04. 2020 10:42
- statistika_je_naj
- Příspěvky: 68
- Reputace: 0
Re: studentovo rozdelenie
Ok no a este by som mal otazku ze v com je rozdiel ked sa pouziva studentovo rozdelenie a ked sa pouziva normalne rozdelenie? Mne to pripada take dost podobne a aj tie hodnoty v tabulkach su mierne podobne. Navyse Studentovo rozdelenie pre velke hodnoty sa blizi k normalnemu tak ja neviem ci je to jedno, asi nie.
Offline
