Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 03. 2020 16:16
Body krivky
Ako dokázať, že krivka  má najviac
má najviac 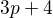 bodov. Pričom
bodov. Pričom 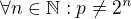 ?
?
Moja idea: Nájdem si nejaký bod v nekonečne, potom položím všetky priamky cez tento bod a pomocou vety od Bezouta spočítam priesečníky s krivkou C. Len ma nenapadá ako nájdem ten bod v nekonečne a ako nájdem všetky priamky prechádzajúce cez tento bod. Budem vďačný za každú radu.
Offline
#2 23. 04. 2020 05:59 — Editoval OiBobik (23. 04. 2020 06:27)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Body krivky
↑ Gauß69:
To je docela rozumná strategie.
1) Počet 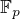 -racionálních přímek v
-racionálních přímek v 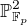 , procházejících nějakým
, procházejících nějakým 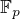 -racionálním bodem
-racionálním bodem  , je totéž, co počet lineárních forem
, je totéž, co počet lineárních forem  s koeficienty v
s koeficienty v 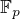 , které můžou takovou přímku definovat, až na násobení skalárem. Ty uvažované formy tedy musí splňovat
, které můžou takovou přímku definovat, až na násobení skalárem. Ty uvažované formy tedy musí splňovat  , tj. vektor
, tj. vektor 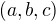 je brán z dvoudimenzionálního
je brán z dvoudimenzionálního 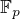 -prostoru, nesmí to být nulový vektor a bere se až na násobek. Krátce řečeno: všechny přímky procházející bodem tvoří projektivní přímku. Jejich počet je tedy roven
-prostoru, nesmí to být nulový vektor a bere se až na násobek. Krátce řečeno: všechny přímky procházející bodem tvoří projektivní přímku. Jejich počet je tedy roven  .
.
2) Zdá se mi, že z toho důvodu není dobré začínat s nějakým náhodným bodem v nekonečnu. Lepší je zvolit nějaký očividný bod na  , třeba
, třeba 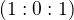 . Takto mi každá nová přímka přímka přidá nejvýše tři nové body, a ne potenciálně čtyři.
. Takto mi každá nová přímka přímka přidá nejvýše tři nové body, a ne potenciálně čtyři.
3) Snad se nepletu, ale jelikož jedna z těch přímek by měla být tečna v bodě 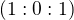 , tj. násobnost dotyku by měla být alespoň
, tj. násobnost dotyku by měla být alespoň  , díky čemuž může ta tečna protnout
, díky čemuž může ta tečna protnout  v nejvýše dvou dalších
v nejvýše dvou dalších 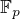 -racionálních bodech; ve výsledku by tedy mělo jít zlepšit ten odhad na
-racionálních bodech; ve výsledku by tedy mělo jít zlepšit ten odhad na  . No a když si dá člověk tu právi tu tečnu spočítat a najít na ní ty body, tak stáhne ten odhad snad i na
. No a když si dá člověk tu právi tu tečnu spočítat a najít na ní ty body, tak stáhne ten odhad snad i na 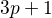 ...
...
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 23. 04. 2020 12:37
Re: Body krivky
↑ OiBobik:
Vdaka, pekne riesenie.
1) Mam aj ja  moznych projektivnych priamok.
moznych projektivnych priamok.
2) Jo sedi to tiez u mna, vyplyva to z vety od Bezouta.
3) Podla vety od Hasse-Weil by mal byt dokonca ten odhad  .
.
Cize pre  je tento odhad este presnejsi ako
je tento odhad este presnejsi ako 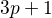 .
.
Offline
#4 24. 04. 2020 02:58
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Body krivky
↑ Gauß69:
Ano, Hasse-Weil dává samozřejmě o dost lepší odhad, taky je to o dost hlubší výsledek než Bézoutova věta na  .
.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline