Matematické Fórum

Frantik88

Zdar,
řeším tu jednu pěknou limitku a nemužu ji vyřešit. Zkoušel jsem ji převést do exponenciálního tvaru, tudíž e na něco, ale vyšlo mi, že limita je nekonečno a správný výsledek je 0.

${\lim}\limits_{x \to \infty} (\frac{3n - 7}{8 + 7n})^n$

halogan · 06. 06. 2009 17:11

Osobní tip: vytkni n z čitatele i jmenovatele a pokráť. Pak ti zbyde (3/7)^n, což konverguje k nule.

Je možné to tak počítat?

Frantik88 · 06. 06. 2009 17:23

Jo, v pohodě, díky...

Pavel Brožek

↑ halogan:

Výsledek je určitě dobře, ale přikláněl bych se k tomu to trochu rozepsat

$\lim_{n \to \infty} $\frac{3n - 7}{8 + 7n}$^n=\lim_{n \to \infty} \textrm{e}^{n\cdot\ln$\frac{3n - 7}{8 + 7n}$}$

Tady je pak postup jasný. (Ten tvůj zkrácený zápis by mohl vést ke špatnému pochopení, např. $\lim_{n\to\infty}$\frac n{n+1}$^n=\lim_{n\to\infty}1^n=1$ , což není dobře.)

ttopi · 06. 06. 2009 18:02

Nebo převést na mou oblíbenou pozoruhodnou limitu s e :-)

MMMartin · 06. 06. 2009 18:22

A nebo použít větu o limitě sevřené posloupnosti a odhadnout to zdola nulou a shora (3/7)^n.

xificurC · 06. 06. 2009 19:39

Alebo si vsimnut vtipne zadanie, kde x ide k nule, takze vysledok je samotne zadanie :)

Asinkan · 07. 06. 2009 12:35

↑ BrozekP:
Můžeš mi říct, jak si došel k tomu, že by to moh někdo pochopit takhle: $\lim_{n\to\infty}$\frac n{n+1}$^n=\lim_{n\to\infty}1^n=1$ ?

Pavel Brožek · 07. 06. 2009 13:18

↑ Asinkan:

Asi takhle: člověk dostane zadání $\lim_{n\to\infty}$\frac n{n+1}$^n$ . Přečte si tady na fóru haloganovu odpověď a řekne si "vytknu n z čitatele i jmenovatele a pokrátím. Pak mi zbyde (1/1)^n, což konverguje k jedničce."

halogan · 07. 06. 2009 14:03

↑ BrozekP:

Vše samozřejmě záleží na úsudku řešitele. Já jsem jen vyřešil, k čemu konverguje "posloupnost" (v R) v mocnině, nedával bych tam rovnítko $\frac{3n - 7}{8 + 7n} = \frac37$ , stejně tak nebudu dávat do rovnítka $\frac{n}{n + 1} = 1$ . Je třeba odlišit konvergenci a rovnost.

Nic to však nemění na tom, že mé řešení zdaleka není univerzální dá se použít jen v krajních případech.

Pavel Brožek · 07. 06. 2009 15:06

↑ halogan:

Vůbec jsem to nemyslel tak, že bys tvrdil $\frac{3n - 7}{8 + 7n} = \frac37$ , pochopil jsem, že to myslíš limitně. Ale nemůžeme jen tak tvrdit, že

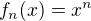$\lim_{n\to\infty}f_n(a_n)=\lim_{n\to\infty}f_n(A)$ , kde $A=\lim_{n\to\infty}a_n$ a f_n jsou nějaké funkce. U funkce $f_n(x)=x^n$ rovnost limit platí, pokud $|A|<1$ (případně rovnost nekonečen pro A>1). Mě to nepřipadá natolik samozřejmé, abychom to mohli zamlčovat. Tak jsem na to chtěl upozornit, aby si toho čtenáři byli vědomi.

Matematické Fórum

#1 06. 06. 2009 17:00 — Editoval Frantik88 (06. 06. 2009 17:00)

Limitka

#2 06. 06. 2009 17:11

Re: Limitka

#3 06. 06. 2009 17:23

Re: Limitka

#4 06. 06. 2009 17:36 — Editoval BrozekP (06. 06. 2009 17:40)

Re: Limitka

#5 06. 06. 2009 18:02

Re: Limitka

#6 06. 06. 2009 18:22

Re: Limitka

#7 06. 06. 2009 19:39

Re: Limitka

#8 07. 06. 2009 12:35

Re: Limitka

#9 07. 06. 2009 13:18

Re: Limitka

#10 07. 06. 2009 14:03

Re: Limitka

#11 07. 06. 2009 15:06

Re: Limitka

Zápatí