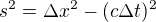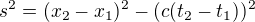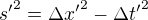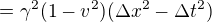Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#76 15. 04. 2020 18:48 — Editoval Zvedavec 4 (16. 04. 2020 12:01)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
Odkladal jsem vzdycky nejakou snahu o vice detilani pochopeni vzorecku pro ten tzv. interval casoprostoru  a tak se k tomu dostavam az ted.
a tak se k tomu dostavam az ted.
Zjistuju ale, ze tedy vlastne popisuje trochu jinym zpusobem o kolik se teleso "v pohybu" prostorem mezi dvema udalostmi vychyluje v case.
Kdyz raketa leti rychlosti v=0.8c, k udalosti B, ktera je vzdalena od udalosti A x=0.8c a dolitne k ni tudiz za t=1s, potom interval casoprostoru bude s=0.6[s]. Tedy v pohledu soustavy "v klidu".
I kdyz v pohledu soustavy "v pohybu" budou hodnoty x' a t' jine nez ty x a t, delka toho intrevalu se nezmeni, tedy bude zase s'=0.6s.
V obou pripadech ale bude snad rychlost v=0.8c. Timhle si 100% jisty nejsem, ale predpokladam, ze tomu tak bude, protoze STR tvrdi, ze se "x" a "t" meni na "x'" a "t'" primerene rychlosti pohybu prostorem a dane vzajemne prostorove vzdalenosti mezi temi udalostmi. Takze "v" by se mela povazovat za stalou.
Vysvetluje se tam, ze "Jestlize je vesmir 4 rozmerny, potom ten interval casoprostoru bude jeden z tech tzv. invariantu", a tedy, ze se jeho delka nebude menit a to, snad maji na mysli, za zadnych okolnosti.
"Kdokoliv bude nejaky interval merit dostane stejnou hodnotu at se pohybuje jakoukoliv rychlosti".
Protoze nevim jak jinak by ho mohli merit pripada mi to, ze tvrdi, ze kdyby jina raketa prolitla mezi temi dvema udalostmi A a B, co jsou x=0.8c od sebe vzdalene, ale letela by jinou rychlosti, treba v=0.7c, vysledek by mel, nejak, zustat stejny, tedy ze s=0.6s.
Sice mi to nedava moc smysl, ale abych se ujistil, jestli to tak je nebo ne, propocital jsem si to:
t'=g(t-vx/c^2)=g(0.8/0.7-0.7x0.8)=1.400 280 084(1.142 857 143-0.56)=1.400 280 084(0.582 857 142)=0.816 163 249s
x'=g(x-vt)=g(0.8-0.7x0.8/0.7)=1.400 280 084(0.8-0.8)=0km
s'^2=x'^2-(vt')^2=0-(0.7x0.816 163 249)^2=>s'=0.571 314 274s
s^2=x^2-(vt)^2=0.8^2-(0.7x0.8/0.7)^2=>s=0s
Protoze to nevychazi, je jasne, ze se tim mysli neco jineho, ale nenapada me vubec co by to mohlo byt.
Mohl by to nekdo objasnit?
Offline
#77 19. 04. 2020 12:58 — Editoval edison (19. 04. 2020 13:01)
Re: Kontrakce Delek
Je to prostá vzdálenost dvou bodů podle Pythagorovy věty, ovšem použitá tak, že jedna ze vstupních vzdáleností je časová. Žádné další složitosti v tom nehledej.
Technická poznámka: Pro nový dotaz zakládej nové téma. Když budeš o tomhle diskutovat na víc stránkách, začne být těžké najít původní dotaz.
Offline
#78 19. 04. 2020 15:35
Re: Kontrakce Delek
Zvedavec 4 napsal(a):
Odkladal jsem vzdycky nejakou snahu o vice detilani pochopeni vzorecku pro ten tzv. interval casoprostoru
a tak se k tomu dostavam az ted.
Zjistuju ale, ze tedy vlastne popisuje trochu jinym zpusobem o kolik se teleso "v pohybu" prostorem mezi dvema udalostmi vychyluje v case.
Kdyz raketa leti rychlosti v=0.8c, k udalosti B, ktera je vzdalena od udalosti A x=0.8c a dolitne k ni tudiz za t=1s, potom interval casoprostoru bude s=0.6[s]. Tedy v pohledu soustavy "v klidu".
I kdyz v pohledu soustavy "v pohybu" budou hodnoty x' a t' jine nez ty x a t, delka toho intrevalu se nezmeni, tedy bude zase s'=0.6s.
V obou pripadech ale bude snad rychlost v=0.8c. Timhle si 100% jisty nejsem, ale predpokladam, ze tomu tak bude
Né, rychlost stejná nebude.
A fyzikální význam časoprostorového intervalu je tzv. vlastní čas (případně by to byla vlastní délka, u nadsvětelných rychlostí) ... vlastní čas je čas který ukáží hodinky na té raketě co letí z bodu A do bodu B (mezi těmi dvěma body - událostmi) ... pokud letí konstantní rychlostí.
Offline
#80 19. 04. 2020 18:06 — Editoval Zvedavec 4 (19. 04. 2020 19:22)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
MichalAld napsal(a):
Né, rychlost stejná nebude.
A fyzikální význam časoprostorového intervalu je tzv. vlastní čas (případně by to byla vlastní délka, u nadsvětelných rychlostí) ... vlastní čas je čas který ukáží hodinky na té raketě co letí z bodu A do bodu B (mezi těmi dvěma body - událostmi) ... pokud letí konstantní rychlostí.
To vim. Tedy tech s=0.6 snad taky znamen, ze 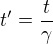 , tedy na kazdou 1s uplynulou v soustave "v klidu" uplyne 0.6s v soustave "v pohybu" z pohledu soustavy "v klidu". Anebo taky, ze se jeji kyvadlo pohne do 60% sveho vykyvu.
, tedy na kazdou 1s uplynulou v soustave "v klidu" uplyne 0.6s v soustave "v pohybu" z pohledu soustavy "v klidu". Anebo taky, ze se jeji kyvadlo pohne do 60% sveho vykyvu.
Intuitivne nemam problem si predstavit, ze kdyz se spoji prostorove vzdalenosti s casovymi intervaly dohromady do tzv. ctryrrozmernosti, potom kdyz se zmeni prostorova vzdalenost x na x', melo by to znamenat, ze casovy interval se zmeni z t na t' tak aby jejich vysledna "smisenina", interval s, zustala stejna v obou pripadech, tedy s=s'.
Jenze, jak tomu rozumim, tam se tvrdi, ze stejna delka toho casoprostoroveho intervalu s=0.6km se zmeri kymkoliv, kdo by cestoval jakoukoliv rychlosti. Asi nezavisle na zadanych hodnotach pro ten konkretni priklad. Tedy ten konkretni vysledek s=0.6km by zustal stejny mezi temi dvema misty.
Co mi neni jasne je kudy by ten kdokoliv cestoval a jakym zpusobem by ten interval s meril aby zustal stejny. Jak se zda, tak to nevychazi, kdyz se pouzije v=0.7c, i kdyz by melo. Protoze to jasne pouzivam spatne, otazkaa je, jakym zpusobem by se to melo pocitat?
Prece ti kosmonauti v rakete, na to aby usoudili, ze se jim vzdalenosti krati budou muset, z jejich hlediska, letet stejnou rychlosti v=0.8c, stejne jako z hlediska pozorovatele "v klidu". Jinak by museli dojit k zaveru, ze dorazili driv, protoze se jim zvetsila rychlost atd. a na tom by nebylo nic relativistickeho.
Ty prapodivne vysledky STR, jako dilatace a kontrakce, jsou prece vysledkem toho, ze se c bere coby nemenna pri ruznych rychlostech pohybu prostorem v ruznych prikladech. A urcite je, protoze, jak tady bylo kdysi vysvetlene, rychlost pohybu telesa prostorem pusobi svymi ucinky na same subatomicke urovni toho telesa, viz kontrakce, na ktere se to asi nejocividneji da chapat a proto i z hlediska toho telesa i pri v rovne skoro c bude ta c stejna, tedy 300 000km/s.
Ale v ramci jedineho prikladu, protoze vlastne existujou jenom dve rozdilne vztazne soustavy, ta nase, tedy "v klidu" a ta druha, tedy "v pohybu", musi snad rychlost pohybu v, at uz z hlediska x, t anebo z hlediska x', t', zustat stejna. Nebo ne?
Offline
#81 19. 04. 2020 20:23
Re: Kontrakce Delek
Možná pomůžou žížaly:
http://utf.mff.cuni.cz/popularizace/ziz … aly-T.html
Tam se zrovna tohle (mimo jiné) hodně polopaticky probírá.
Offline
#82 20. 04. 2020 16:12
Re: Kontrakce Delek
Zvedavec 4 napsal(a):
To vim. Tedy tech s=0.6 snad taky znamen, ze
, tedy na kazdou 1s uplynulou v soustave "v klidu" uplyne 0.6s v soustave "v pohybu" z pohledu soustavy "v klidu". Anebo taky, ze se jeji kyvadlo pohne do 60% sveho vykyvu.
To je hezký, ale ty hodiny jsou taky na nějakém místě. A to musíme zohlednit také. Pro jednu soustavu jsou hodiny pořád na stejném místě (třeba u tebe doma na stole), ale pro jinou soustavu se už pohybují. Jenže čas měřený v té druhé soustavě není ten, co ukazují ty pohybující se hodiny, ale čas, co ukazují stojící ... v každém bodě soustavy.
Offline
#84 20. 04. 2020 16:32
Re: Kontrakce Delek
Můžeš si tam klidně dosadit, pokud tě baví počítání ... pokud to vyjde v písmenkách, musí to vyjít i pro konkrétní čísla.
Jen nezapomeň, že tak jak jsem to napsal musíme vzdálenost měřit v sekundách (světelných sekundách), tedy vzdálenost v metrech musíme podělit c. Stejně tak rychlost. Klidně si tam ta "céčka" dopiš, ale je to jen práce navíc...
Co znamenají časoprostorové souřadnice (zejména tedy souřadný čas) jsem se ti už několikrát pokouše vysvětlit, ale je to stejně marný...pokud to chceš chápat intuitivně, tak je to tak, že v každém bodě souřadné soustavy musí být jedny hodiny ... a pokud se soustava pohybuje, tak se pohybují taky. Pokud to "intuitivně" nedáváš, tak máš asi smůlu, jinak to nejde.
Offline
#86 23. 04. 2020 23:05 — Editoval Zvedavec 4 (24. 04. 2020 01:03)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
MichalAld napsal(a):
Zvedavec 4 napsal(a):
To vim. Tedy tech s=0.6 snad taky znamen, ze
, tedy na kazdou 1s uplynulou v soustave "v klidu" uplyne 0.6s v soustave "v pohybu" z pohledu soustavy "v klidu". Anebo taky, ze se jeji kyvadlo pohne do 60% sveho vykyvu.
To je hezký, ale ty hodiny jsou taky na nějakém místě. A to musíme zohlednit také. Pro jednu soustavu jsou hodiny pořád na stejném místě (třeba u tebe doma na stole), ale pro jinou soustavu se už pohybují. Jenže čas měřený v té druhé soustavě není ten, co ukazují ty pohybující se hodiny, ale čas, co ukazují stojící ... v každém bodě soustavy.
Ano, i tohle mi je jeste znamo, jestli mi je jasne, o cem mluvis, protoze se to dost tezko popisuje tak aby to bylo dobre srozumitelne.
Hodnoty souradneho casu jsou potreba znat v kazde z tech dvou soustav. Tedy v kazde z tech soustav hodnoty jejiho vlastniho souradneho casu.
Hodiny rozmistene skrz prostor v jedne z tech soustav, treba soustavy zvane "v klidu", jsou ty hodiny, jejichz cas v te soustave "v klidu" ubiha a jimz se ta soustava ridi, ale tahle "sbirka" hodin z pohledu te soustave druhe, zvane "v pohybu", je v pohybu.
A jelikoz se ta zminena "sbirka" pohybuje z pohledu soustavy zvane "v pohybu", cas te zminene "sbirky" soustavy zvane "v klidu" neni casem, ktery je meren a ubiha v te soustave zvane "v pohybu", protoze se ta "sbirka" vuci ni pohybuje. A proto ta soustava zvana "v pohybu" musi mit svou vlastni "sbirku" rozmistenou skrze svuj vlastni prostor, jejimz casem se pak musi ridit.
Pisu to jenom proto aby's vedel, ze tohle mi je jasne.
Rozdil v casech mezi temi dvema "sbirkami" se pocita, jak se tvrdi, pomoci toho tzv. "rozdilu fazi", tedy  . Tedy o tolik jdou v urcitem konkretnim miste hodiny jedne z tech "sbirek" napred/pozadu vuci hodinam te druhe "sbirky".
. Tedy o tolik jdou v urcitem konkretnim miste hodiny jedne z tech "sbirek" napred/pozadu vuci hodinam te druhe "sbirky".
Offline
#87 23. 04. 2020 23:38 — Editoval Zvedavec 4 (24. 04. 2020 05:10)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
MichalAld napsal(a):
Jinak, pokud si to chceš spočítat, je to celkem snadné.
Pokud budeme uvažovat přirozenou volbu jednotek, tedy že c=1, tak:
a analogicky
Diky moc za tenhle detajlni rozpis, ale tady to budu muset vzdat. Je to moc zamotane.
Uvazuju na zaklade me otazky, a sice, jak by pozorovatel v rakete s rychlosti v=0.7c zpozoroval ten interval casoprostoru zmereny pri rychlosti v=0.8s, ze by byl stejne delky?
Protoze treba v 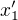 a
a 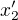 , o kterych bych si myslel, zeby mely mit rozlicne rychlosti, tedy
, o kterych bych si myslel, zeby mely mit rozlicne rychlosti, tedy  a
a 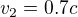 , mas pro rychlosti stejne hodnoty, to uz se lisi od me predstavy, co znamena ten jejich vyrok, ze "....kdokoliv by se pohyboval jakoukoliv rychlosti by ten interval zmeril stejne dlouhy....".
, mas pro rychlosti stejne hodnoty, to uz se lisi od me predstavy, co znamena ten jejich vyrok, ze "....kdokoliv by se pohyboval jakoukoliv rychlosti by ten interval zmeril stejne dlouhy....".
Myslel bych si taky, zeby se ve vypoctu pro 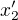 od
od 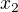 , ktera by mela byt pri v=0.7c
, ktera by mela byt pri v=0.7c 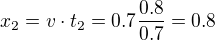 melo odecitat
melo odecitat  atd.
atd.
Mas tam taky stejnou gamu pro 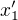 a
a 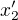 , prestoze bych si myslel, ze by mely byt rozlicne, jestlize
, prestoze bych si myslel, ze by mely byt rozlicne, jestlize 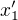 pochazi z
pochazi z 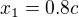 a
a 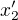 pochazi z
pochazi z 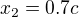 , atd.
, atd.
Budu to zkratka brat, ze tomu tak bude.
Offline
#88 24. 04. 2020 00:52 — Editoval Zvedavec 4 (24. 04. 2020 04:20)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
↑ MichalAld:
Ten "interval casoprostoru" je snad dany primo tim zakladnim vzoreckem, ze  . A vyznam toho se asi musi vysvetlit podle toho, jak to vychazi.
. A vyznam toho se asi musi vysvetlit podle toho, jak to vychazi.
Tedy, ze se teleso "v pohybu" pohne nejenom mezi body A a B, tedy B-A=x, ale taky se pohne mezi casovymi okamziky 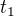 a
a 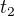 , tedy
, tedy  .
.
Protoze oboji, tedy jak to (x), tak to (ct) vychazi v [km], mel by i ten interval byt taky v [km], prestoze slovo "interval" svadi k tomu aby se o nem smyslelo ve vterinach. Ale to je asi tim, ze, jak jsem se docet, v STR neni rozdil mezi kilometrama a vterinama.
To, ze s=a je z intuitivniho hlediska jasne. Protoze slovo interval naznacuje, ze se jedna o casovy usek, nazev "Interval casoprostoru" by se mel chapat, coby cisty casovy usek casoprostoru.
Napriklad, jestlize pri rychlosti s gamou=2 vychazi ten interval s=300 000km, melo by tech 300 000km byt, podle toho nazvu, cistym casovym usekem, tedy intervalem. Pohyb rakety muze byt jenom casoprostorem a tudiz tech zbyvajicich 600 000km muze byt jenom pohyb fotonu cistym prostorem 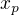 . Tak bych to intuitivne chapal.
. Tak bych to intuitivne chapal.
A protoze je tim vysloven zakladni princip STR, ze cim vic se teleso "v pohybu" premisti prostorem, v zavislosti na rychlosti "v" sveho pohybu, tim min se premisti casem "t" a naopak, myslim si, ze mi je podstata toho intervalu celkem jasna.
Offline
#89 24. 04. 2020 16:12
Re: Kontrakce Delek
Zvedavec 4 napsal(a):
Diky moc za tenhle detajlni rozpis, ale tady to budu muset vzdat. Je to moc zamotane.
No tak to vzdej ... je to pořád lepší než si myslet, že když polovinu členů vynecháš, že pořád dostaneš stejný výsledek...
Offline
#90 24. 04. 2020 16:12 — Editoval Zvedavec 4 (24. 04. 2020 16:15)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
MichalAld napsal(a):
Jinak, pokud si to chceš spočítat, je to celkem snadné.
Pokud budeme uvažovat přirozenou volbu jednotek, tedy že c=1, tak:
a analogicky
Mozna se tady, Michale, snazis poukazat na to, a tim to zduraznit, ze protoze udalost "B" od nas vzdalena lezi v bode "B", tak behem te doby, co k ni leti raketa, se ten bod "B" i s tou udalostii "B" vzdaluji od te rakety v case a to rychleji, nez se v case premistuje ta letici raketa sama. A tedy to vysledne 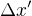 je mozna vysledkem nejenom rozdilu mezi nejakymi
je mozna vysledkem nejenom rozdilu mezi nejakymi 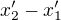 , tedy puvodnim a vyslednym umistenim toho bodu "B" v prostoru, ale taky vysledkem rozdilu mezi
, tedy puvodnim a vyslednym umistenim toho bodu "B" v prostoru, ale taky vysledkem rozdilu mezi  , tedy rozdilu jeho dvou casovych okamziku, tedy premisteni se casem (toho bodu).
, tedy rozdilu jeho dvou casovych okamziku, tedy premisteni se casem (toho bodu).
A to same potom, to vysledne  bude mit v sobe obsazeny vliv prostoroveho umisteni, protoze se tady jedna o ten tzv. "casoprostor" coby nerozdelitelny celek.
bude mit v sobe obsazeny vliv prostoroveho umisteni, protoze se tady jedna o ten tzv. "casoprostor" coby nerozdelitelny celek.
Offline
#92 25. 04. 2020 13:35
Re: Kontrakce Delek
Zvedavec 4 napsal(a):
MichalAld napsal(a):
Jinak, pokud si to chceš spočítat, je to celkem snadné.
Pokud budeme uvažovat přirozenou volbu jednotek, tedy že c=1, tak:
a analogickyMozna se tady, Michale, snazis poukazat na to, a tim to zduraznit, ze protoze udalost "B" od nas vzdalena lezi v bode "B", tak behem te doby, co k ni leti raketa, se ten bod "B" i s tou udalostii "B" vzdaluji od te rakety v case a to rychleji, nez se v case premistuje ta letici raketa sama.
Kdepak - pro pozorovatele v raketě se raketa nikam neblíží ... pro pozorovatele v raketě ta raketa stojí ... a naopak se k němu blíží ten bod B. Případně se teda vzdaluje ...
Už jsem to psal 100x, raketa není soustava, raketa je "někde", takže jak bod A tak i bod B mohou být zcela libovolně buď před ní, nebo za ní.
Soustava je naproti tomu nekonečně velká ...zabírá celý prostor i čas ...a na časoprostorový interval mezi dvěma událostmi nemá přítomnost (či absence) nějaké rakety žádný vliv.
Offline
#93 25. 04. 2020 13:46
Re: Kontrakce Delek
Zvedavec 4 napsal(a):
↑ MichalAld:
Ten "interval casoprostoru" je snad dany primo tim zakladnim vzoreckem, ze. A vyznam toho se asi musi vysvetlit podle toho, jak to vychazi.
Hlavní problém je ten, že ten s^2 může vyjít kladný i záporný.
Třeba pro dvě události, které jsou od sebe v prostoru metr a v čase sekundu to určitě záporné vyjde.
A odmocninu ze záporného čísla je trochu problém vypočítat ... tak aby představovala něco fyzikálního.
Takže se to dělá tak, že se vybere jedna z variant, vždy taková, aby výsledek vyšel kladný.
nebo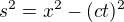
Akorát si musíme pamatovat, který vzorec jsme použili. Interval vypočtený podle prvního vztahu se nazývá "času-podobný" a interval vypočtený podle druhého "prostoru-podobný".
Z toho je už celkem zřejmé, že fyzikální význam prvního intervalu bude nejspíš čas (i když to vyjde v metrech), a fyzikální význam druhého bude vzdálenost.
No ... první interval odpovídá pohybu podsvětelnou rychlostí, a druhý pohybu nadsvětelnou ... jenže s tím se v našem světě nesetkáváme, takže dvě události, mezi kterými je prostoru-podobný interval nemohou být kauzálně propojeny - jedna nemůže být příčinou druhé. Takže je do jisté míry jedno, co takový interval představuje fyzikálně.
Fyzikální význam času-podobného intervalu je tzv. vlastní čas ... čas který uběhne třeba ve tvé raketě, která se přemístí z události A do údálosti B konstantní rychlostí.
Offline
#94 25. 04. 2020 18:27 — Editoval Zvedavec 4 (25. 04. 2020 18:38)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
Michale, asi jsme si nerozumneli. Zakladni moje otazka byla zalozena na spatne predstave, ze kdyz se rekne, ze "interval casoprostoru" bude stejny pro "....kohokoliv at uz leti jakoukoliv rychlosti....", melo by to znamenat ze:
kdyz v=0.8c a t=1s, jasne by vzdalenost mezi body s udalostmi A a B byla x=0.8c[km]. A protoze 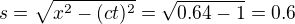 , potom jasne ten interval bude s=0.6[km nebo vterin].
, potom jasne ten interval bude s=0.6[km nebo vterin].
Kdyz jina raketa poleti soucasne z toho sameho bodu A do toho sameho bodu B, tak by ten interval, "....protoze ta kterakoliv jina raketa leti jakoukoliv jinou rychlosti....", musela zmerit stejny, tedy s=0.6[km nebo vterin].
A tedy, kdyz v=0.7c, tak protoze vzdalenost mezi temi body by mela zustat stejna (jinak se nemuze mluvit o stejnem intervalu), vzdalenost mezi A a B by se nadale rovnala  [km], ale potom
[km], ale potom 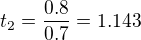 s, pro tu druhou raketu s rychlosti v=0.7c.
s, pro tu druhou raketu s rychlosti v=0.7c.
Ale jak videt,  a z toho pak
a z toho pak  , tedy je uplne jiny a to i presto, ze porad
, tedy je uplne jiny a to i presto, ze porad 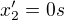 , tak jako to puvodni
, tak jako to puvodni 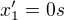 , a taky v tomhle pripade,
, a taky v tomhle pripade, 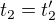 a tedy
a tedy 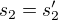 . Ale to je pocetne normalni.
. Ale to je pocetne normalni.
Kdyz se nad tim ted zamyslim, tak si uvedomuju, ze protoze s=0.6 je to, ceho se musi docilit, tak potom se tedy nemuze pouzit, jak jsem si puvodne predstavoval,  , protoze aby ten interval zas vysel totozny, potom by zase muselo platit, ze
, protoze aby ten interval zas vysel totozny, potom by zase muselo platit, ze 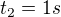 , jako v tom prvnim pripade pri v=0.8c a byl by to tedy ten samy priklad.
, jako v tom prvnim pripade pri v=0.8c a byl by to tedy ten samy priklad.
Otazkou potom treba bude, proc by se mela menit prostorova vzdalenost "x" jenom proto, ze rychlost "v" bude jina? To totiz odporuje puvodnimu prohlaseni, ze ten interval bude zmereny coby stejny.
Odpovedi je jasne to, ze by to jinak nevyslo pocetne. To znamena, ze se musi zmenit oba, tedy jak "x" tak i "t" aby se mohl dostat stejny "s". Takze potom to ztraci smysl, protoze tim je prohlaseni o tom, ze ten interval zustane stejny, vyresene, a sice coby nesmyslne.
Jenom mi jeste neni jasne, jak dostat ty zmenene hodnoty "x" a "t" aby odpovidaly urcite rychlosti, jako treba v=0.7c a taky s=0.6, protoze to vypada jako 1 znama, tedy s=0.6, a 2 nezname, tedy ty "x" a "t", a to se snad spocitat neda?
Kdyby se reklo, ze protoze v=0.7 a t=1s a tedy x=0.7, nebyl by to uplne jiny pripad?
Ve Tvych prvnich 5 vzoreckach, kdybych si myslel, ze 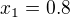 a
a 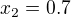 , potom
, potom 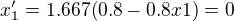 a
a 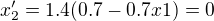 . Pak
. Pak 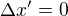 .
.
Potom 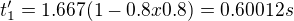 a
a 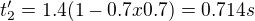 . Pak, co by se treba dosadilo za "v" a co za gamu pro vypocet
. Pak, co by se treba dosadilo za "v" a co za gamu pro vypocet  ? Asi to tedy myslis jinak.
? Asi to tedy myslis jinak.
Offline
#96 25. 04. 2020 18:49 — Editoval Zvedavec 4 (25. 04. 2020 18:50)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
MichalAld napsal(a):
Kdepak - pro pozorovatele v raketě se raketa nikam neblíží ... pro pozorovatele v raketě ta raketa stojí ... a naopak se k němu blíží ten bod B. Případně se teda vzdaluje ...
Už jsem to psal 100x, raketa není soustava, raketa je "někde", takže jak bod A tak i bod B mohou být zcela libovolně buď před ní, nebo za ní.
Soustava je naproti tomu nekonečně velká ...zabírá celý prostor i čas ...a na časoprostorový interval mezi dvěma událostmi nemá přítomnost (či absence) nějaké rakety žádný vliv.
Tyhle body mi jsou davno jasne. Prece tou raketou, coby soustavou "v pohybu", protoze v pohybu je (prestoze je soustavou "v klidu" pro ty kosmonauty, co v ni jsou) vuci te soustave druhe, jine, tedy nasi, tedy soustave "v klidu", se mysli vsechno co k ni patri. Tedy treba to jinak se menici jeji okoli/pozadi, ktere se meni jinak pro ty kosmonauty nez pro nas, v te soustave nasi, tedy soustave "v klidu", pro kterou se vlastne (jakoby vubec) nemeni.
Offline
#97 25. 04. 2020 18:54
Re: Kontrakce Delek
Zvedavec 4 napsal(a):
Michale, asi jsme si nerozumneli. Zakladni moje otazka byla zalozena na spatne predstave, ze kdyz se rekne, ze "interval casoprostoru" bude stejny pro "....kohokoliv at uz leti jakoukoliv rychlosti....", melo by to znamenat ze:
kdyz v=0.8c a t=1s, jasne by vzdalenost mezi body s udalostmi A a B byla x=0.8c[km]. A protoze, potom jasne ten interval bude s=0.6[km nebo vterin].
Ale vždyť to vůbec není pravda, co říkáš .. ty události A a B vůbec nesouvisejí s nějakou rychlostí v, kterou se nějaký pozorovatel pohybuje.
Události jsou prostě události ... třeba že dnes v 16:30 UTC si Alice v Praze uvařila kafe a Bob v New Yorku v 16:31 UTC si vypil čaj...
S nějakou raketou, co se pohybuje rychlostí 0.7c to vůbec nesouvisí... na Alici a Boba a jejich nápoje může koukat tisíce pozorovatelů z tisíců různých raket...
Offline
#98 25. 04. 2020 18:56
Re: Kontrakce Delek
Já už ti to jednou napsal, co znamená ta invariance časoprostorového intervalu, totiž tady ↑ MichalAld:, ty jsi napsal, že je to na tebe moc složité, a že to vzdáváš...a já ti napsal, že jednodušším způsobem to bohužel nejde.
Takže pokud se tímhle nedokážeš probrat, nemá smysl hledat nějaké alternativní vysvětlení, protože prostě NEMŮŽE BÝT SPRÁVNÉ.
Offline
#99 25. 04. 2020 19:02
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
MichalAld napsal(a):
Zvedavec 4 napsal(a):
Michale, asi jsme si nerozumneli....
Jistě, když nedává smysl otázka, nebude dávat smysl ani odpověď...
Co tim tedy myslej, ze "....interval bude stejny at uz se leti jakoukoliv rychlosti…."?
Offline
#100 25. 04. 2020 19:21 — Editoval Zvedavec 4 (25. 04. 2020 19:45)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
Dobry. Tvou predchozi odpoved nachazim az ted, co uz jsem poslal tu mou posledni.
Offline