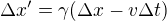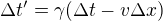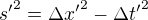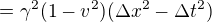Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#101 25. 04. 2020 20:23
Re: Kontrakce Delek
Zvedavec 4 napsal(a):
MichalAld napsal(a):
Zvedavec 4 napsal(a):
Michale, asi jsme si nerozumneli....
Jistě, když nedává smysl otázka, nebude dávat smysl ani odpověď...
Co tim tedy myslej, ze "....interval bude stejny at uz se leti jakoukoliv rychlosti…."?
Nevím, platí pouze to, že časoprostorový interval je stejný pro všechny pozorovatele, což znamená, že je stejný v každé vztažné soustavě ... (a soustavy se vůči sobě mohou navzájem pohybovat).
Offline
#102 25. 04. 2020 20:25 — Editoval MichalAld (25. 04. 2020 20:27)
Re: Kontrakce Delek
Zvedavec 4 napsal(a):
MichalAld napsal(a):
Kdepak - pro pozorovatele v raketě se raketa nikam neblíží ... pro pozorovatele v raketě ta raketa stojí ... a naopak se k němu blíží ten bod B. Případně se teda vzdaluje ...
Už jsem to psal 100x, raketa není soustava, raketa je "někde", takže jak bod A tak i bod B mohou být zcela libovolně buď před ní, nebo za ní.
Soustava je naproti tomu nekonečně velká ...zabírá celý prostor i čas ...a na časoprostorový interval mezi dvěma událostmi nemá přítomnost (či absence) nějaké rakety žádný vliv.Tyhle body mi jsou davno jasne. Prece tou raketou, coby soustavou "v pohybu", protoze v pohybu je
Není. Není o nic víc v pohybu než ta druhá...
Stejně tak může být v pohybu ta "naše" soustava. Pro nás jsou v pohybu oni, pro ně jsme v pohybu my.
Jo, a události, ty se nepohybují.
Offline
#103 26. 04. 2020 15:53
Re: Kontrakce Delek
Ještě uvednu jednoduchý příklad časoprostorového intervalu - aby bylo jasné, že se to může týkat úplně obyčejných věcí.
Takže třeba někde ve Svitavách si Alice rozsvítí světlo, v 7:00 UTC, a Bob v Brně si rozsvítí o sekundu později. Vzdálenost ze Svitav do Brna je zhruba 100km, aby se to dobře počítalo. Takže máme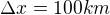
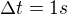
Časoprostorový interval bude tedy (zvolíme ten vzorec, co dává kladný výsledek - takže zjevně):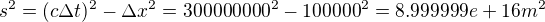

Je to taková nicneříkající divnovzdálenost, takže to raději "převedeme na sekundy" (= podělíme c) a dostaneme
Tedy téměř jednu sekundu. Co to znamená fyzikálně? Když bychom ze Svitav do Brna postavili dálnici, a hezky rovnou, a poslali po ní automobil, který pojede přesně takovou rychlostí, aby při události A vyrazil a při události B právě dorazil - musel by tedy jet těch 100km/s - a do kufru mu naložili hodiny, aby mohly změřit, jak dlouho bude na cestě - tak ty hodiny ukáží přesně tenhle čas, těch 0.9999... s.
Říká se tomu vlastní čas. A odpovídá to tomu časoprostorovému intervalu.
Auto samozřejmě nemusjí jet nutně konstantní rychlostí, může jet polovinu cesty rychleji a druhou pomaleji ... potom bude jeho vlastní čas kratší. Nejdelšího vlastního času dosáhne tím, že pojede konstantní rychlostí. Cokoliv udělá jiného, mu vlastní čas zkrátí.
Je to (až na jeden detail) podobné, jako vzdálenost dvou bodů v prostoru. Obecně je můžeme spojit libovolnou čarou - ale všechny čáry budou delší, než když je spojíme přímkou. Délka přímky která spojuje dva body - to je vzdálenost v prostoru.
V časoprostoru je to víceméně stejné ... "nejkratší spojnici" odpovídá pohyb konstantní rychlostí. Ovšem díky té zvláštní metrice mezi prostorem a časem, té "Pythagorově větě se znaménkem minus" můžeme dosáhnout toho, že časoprostorový interval bude nulový, či dokonce záporný (správně tedy jeho druhá mocnina bude záporná). To v prostoru nemá absolutně žádný ekvivalent.
Nenní velký problém vyrobit takový interval (záporný) ... stačí aby si naše Alice a Bob nerozsvítili světla se sekundovým odstupem, ale třeba s mikrosekundovým. Nic tomu nebrání (budou li mít dostatečně přesné hodinky).
Offline
#104 04. 05. 2020 17:23
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
MichalAld napsal(a):
Auto samozřejmě nemusjí jet nutně konstantní rychlostí, může jet polovinu cesty rychleji a druhou pomaleji... potom bude jeho vlastní čas kratší. Nejdelšího vlastního času dosáhne tím, že pojede konstantní rychlostí. Cokoliv udělá jiného, mu vlastní čas zkrátí.
Je to (až na jeden detail) podobné, jako vzdálenost dvou bodů v prostoru. Obecně je můžeme spojit libovolnou čarou - ale všechny čáry budou delší, než když je spojíme přímkou. Délka přímky která spojuje dva body - to je vzdálenost v prostoru.
V časoprostoru je to víceméně stejné ... "nejkratší spojnici" odpovídá pohyb konstantní rychlostí. Ovšem díky té zvláštní metrice mezi prostorem a časem, té "Pythagorově větě se znaménkem minus" můžeme dosáhnout toho, že časoprostorový interval bude nulový, či dokonce záporný (správně tedy jeho druhá mocnina bude záporná). To v prostoru nemá absolutně žádný ekvivalent.
Michale, jen tak na upresnenou, nesplet jsi se tady? Tyhle dva udaje se zdaji byt v rozporu.
Offline
#105 04. 05. 2020 21:17 — Editoval MichalAld (04. 05. 2020 21:27)
Re: Kontrakce Delek
Zmínil jsem, že "až na jeden detail"... každopádně je to ta, jak jsem napsal ... pokud pojedeme po delší dráze, bude vlastní čas kratší.
Proto tu "nejkratší spojnici" píšu v uvozovkách. Ona je ve skutečnosti nejdelší ... jenže se to trochu špatně představuje.
Prostě to 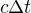 je vždycky stejné (nemáme žádný způsob, jak si udělat "zajížďku v čase, čas má jen jednu dimenzi", zatímco to
je vždycky stejné (nemáme žádný způsob, jak si udělat "zajížďku v čase, čas má jen jednu dimenzi", zatímco to 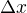 může být delší, když to vezmeme obloukem, takže se nám pak ten časoprostorový interval zkracuje.
může být delší, když to vezmeme obloukem, takže se nám pak ten časoprostorový interval zkracuje.
Ale tohle už nenazýváme časoprostorovým intervalem, nýbrž "délkou" nějaké tzv. světočáry (to je ekvivalent křivky v časoprostoru). Interval ("vzdálenost") je to jen když je to spojené "přímkou".
Vše co píšu v uvozovkách jsou pojmy co se používají ve 3D prostoru. Já přesně ani nevím, jak se správně jmenují jejich ekvivalenty v časoprostoru - a když to nevím já, nebudeš to vědět ani ty, takže bys mi stejně moc nerozuměl. Tak to píšu takto.
Offline
#106 15. 05. 2020 19:19
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
Zvedavec 4 napsal(a):
MichalAld napsal(a):
Auto samozřejmě nemusjí jet nutně konstantní rychlostí, může jet polovinu cesty rychleji a druhou pomaleji... potom bude jeho vlastní čas kratší. Nejdelšího vlastního času dosáhne tím, že pojede konstantní rychlostí. Cokoliv udělá jiného, mu vlastní čas zkrátí.
Michale, kdybych si to chtel overit intuitivne, tak potom kdyby se pohyboval po dobu 0.9t rychlosti 101km/s, pak by ujel 90.9km a kdyby pak dojel zbytek, tedy 0.1t, rychlosti 99km/s, potom by ujel 9.9km.
Celkove by tedy ujel 90.9+9.9=100.8km, tedy by dojel dal. Proto by jeho prumerna rychlost musela byt vetsi a rychlost plynuti jeho casu by se tim, z pohledu te druhe soustavy, musela zpomalit, a protoze, jak se docitam,  , tak i to T by se muselo zmensit. Takze by bylo kratsi nez pri rychlosti stale. Takze v tomhle pripade by se stalou rychlosti docilil delsi cas T.
, tak i to T by se muselo zmensit. Takze by bylo kratsi nez pri rychlosti stale. Takze v tomhle pripade by se stalou rychlosti docilil delsi cas T.
Ale, na druhou stranu, kdyby jel po dobu 0.1t rychlosti 101km/s, ujel by 10.1km a potom po dobu 0.9t rychlosti 99km/s, ujel by 89.1km.
Dohromady by tedy ujel 99.2km, tedy by dojel min. Proto by jeho prumerna rychlost byla mensi a tedy rychlost plynuti jeho casu by, z pohledu te soustavy druhe, byla vetsi.
Ale tady potom, pri zrychleni plynuti jeho casu by se taky T musela zvetsit. Takze by byla vetsi nez pri stale rychlosti. A tedy v tomhle pripade by se stalou rychlosti NEdocililo delsiho casu T.
Tak jak se z toho vseho da usoudit, ze pri stale rychlosti bude jeho T nejdelsi?
Protoze se tady jedna o interval casoprostoru asi to vezi v nem, ale momentalne mi neni jasne jak.
Jestlize 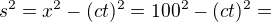 299,999.983 3km;
299,999.983 3km; 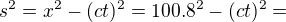 299,999.983 1km;
299,999.983 1km; 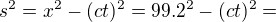 299,999.983 6km!
299,999.983 6km!
Takze to spis vypada, ze pri mensi rychlosti se v casoprostoru dojede dal, protoze ten jeho interval bude vetsi a pri vetsi se dojede do vzdalenosti kratsi, protoze ten interval bude kratsi.
Ale ty tady pises o vlastnim case T a neni mi jasne, jak presne do toho pocetne zapada.
Jestli to muzes objasnit pouzitim tehle uvahy, muze to pomoct. Nakonec to muze byt obsazene v techhle jednoduchych poctech.
Offline
#107 03. 06. 2020 22:49 — Editoval Zvedavec 4 (03. 06. 2020 23:40)
- Zvedavec 4

- Příspěvky: 237
- Reputace: -1
Re: Kontrakce Delek
MichalAld napsal(a):
Jinak, pokud si to chceš spočítat, je to celkem snadné.
Pokud budeme uvažovat přirozenou volbu jednotek, tedy že c=1, tak:
a analogicky
a časoprostorový interval
a když rozepíšeme to gamma, tak
Michale, když se ted' znovu podívám na tenhle tvůj opravdu fascinující rozbor toho, jak ten vzoreček pro interval časoprostoru vzniká, protože jsem si s tím v ten čas nechtěl lámat hlavu, tak je hned na jeho začátku vidět, že situace, kdy raketa poletí oklikou, může vzniknout taky takhle, tedy že se, jak to popisuješ, bude měnit  a s nim
a s nim  při stálé rychlosti
při stálé rychlosti  , coz jsem v tu dobu nepodchytil, protože jsem o tom přemýšlel čistě přímočaře, tedy intuitivně a ani mne v tu dobu nenapadlo, že interval časoprostoru musí zahrnovat, pro tu "jakoukoliv rychlost", let oklikou a to navíc ne změnou rychlosti, ale změnou
, coz jsem v tu dobu nepodchytil, protože jsem o tom přemýšlel čistě přímočaře, tedy intuitivně a ani mne v tu dobu nenapadlo, že interval časoprostoru musí zahrnovat, pro tu "jakoukoliv rychlost", let oklikou a to navíc ne změnou rychlosti, ale změnou  a
a  .
.
I když to je opravdu pěkný rozbor, pro nematematiky se zdá jednodužší to zkoumat intuitivně, pokud se bez početních vzorečků dá obejít, protože navíc s těmi přidanými rozdíly mezi dvěma údajema ve formě  je to pak ještě o to komplikovanější a právě to mě v ten čas odradilo, a proto mi taky v tom zamotanci nedošlo to jasně logický, že se ten výrok z wiki nemůže týkat situace, kdy
je to pak ještě o to komplikovanější a právě to mě v ten čas odradilo, a proto mi taky v tom zamotanci nedošlo to jasně logický, že se ten výrok z wiki nemůže týkat situace, kdy  , ale jenom situace, ve které
, ale jenom situace, ve které  !
!
Pohled z čistě početních vzorců, pokud' úroven' matematiky neumožní si je dát dohromady hned na první pohled, je tedy zbytečně slozitý a zavádějící, i když někdy jejich použití je to tzv. "nezbytné zlo".
Offline