Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 04. 2020 18:47 — Editoval Kája2 (27. 04. 2020 18:55)
Vektorový podprostor
Dobrý den,
mám zadánu úlohu: Mějme dán vektorový prostor  se skalárním součinem
se skalárním součinem 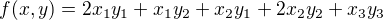 .Ukažte, že
.Ukažte, že 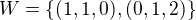 se standardně zavedenými operacemi je podprostem vektorového prostoru
se standardně zavedenými operacemi je podprostem vektorového prostoru  .
.  je evidentně neprázdná, ale například
je evidentně neprázdná, ale například 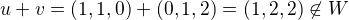 nebo ano?Mám dokázat , že je podprostorem,ale již tady mi to selže. Mohu poprosit o radu?
nebo ano?Mám dokázat , že je podprostorem,ale již tady mi to selže. Mohu poprosit o radu?
Offline
