Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 04. 2020 16:47
Kombinatorika - karty
Zdravím,
mám problém s následující úlohou.
V balíčku je 6 karet, po dvou od každé ze tří barev.
Karty se náhodně rozdělí mezi hráče A,B,C.
Pravděpodobnost, že
Alespoň jeden ze tří hráčů bude mít karty stejné barvy.
Nevím, jak na to, zkusil jsem, že by dostal první hráč jakoukoliv  a následně tu jednu
a následně tu jednu  (téže barvy), a potom libovolně rozdat. Vychází mi 1/5, ovšem výsledek by měl být 7/15.
(téže barvy), a potom libovolně rozdat. Vychází mi 1/5, ovšem výsledek by měl být 7/15.
Díky za pomoc!
Offline
- (téma jako vyřešené označil(a) Sikys)
#2 29. 04. 2020 17:12 — Editoval david_svec (29. 04. 2020 17:14)
- david_svec
- Příspěvky: 435
- Pozice: student
- Reputace: 13
Re: Kombinatorika - karty
↑ Sikys:
Zdravím,
pravděpodobnost, že všichni budou mít RŮZNÉ karty je: 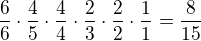
první má na výběr z 6 možností pro první kartu, zbývá 5 pro druhou, z nichž si může vybrat jenom 4, aby neměl stejnou kartu jako tu první; druhý má na výběr už jenom ze 4 možností pro první kartu, zbudou 3 karty ze kterých si může vybrat pouze 2 atd...
Tohle je jev opačný, jak tedy vypočítám pravděpodobnost aby alespoň jeden měl karty stejné barvy?
Offline
#3 29. 04. 2020 17:26
#4 29. 04. 2020 17:37
- david_svec
- Příspěvky: 435
- Pozice: student
- Reputace: 13
Re: Kombinatorika - karty
↑ Sikys:
Měj se. :-)
Offline

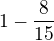 .
.