Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 05. 2020 21:00
- Prokop Ohlídal

- Příspěvky: 26
- Pozice: Student
- Reputace: 1
Energie kondenzátoru
Zdravím,
mám menší dotaz ohledně jednoho úkolu, který zní:
Jak se změní energie kondenzátoru, jestliže jeho náboj zvětšíme n-krát?
Příklad jsem řešil jako 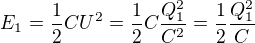 .
.
Poté jsem určil, že 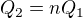 a energii s n-násobkem
a energii s n-násobkem 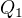 vypočítal jako:
vypočítal jako: 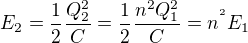 .
.
Výsledek tedy zní: zvětší-li se náboj kondenzátoru n-krát, jeho energie se zvětší  -krát, což je správně.
-krát, což je správně.
Poté jsem ale chtěl zkusit jiný způsob a místo  jsem zaměnil
jsem zaměnil  tzn.:
tzn.: 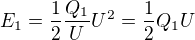 a poté
a poté 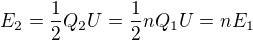 .
.
To je jiný výsledek, protože by to znamenalo, že se energie zvýší tolikrát, kolikrát velikost náboje..nemůžu přijít na to, proč to tak je nebo kde dělám chybu..
Předem děkuji za odpověď:)
Offline
- (téma jako vyřešené označil(a) Prokop Ohlídal)
#2 07. 05. 2020 22:38
Re: Energie kondenzátoru
U je ve vzorci v druhé mocnině, vše ostatní v první. Toť vše:-)
Příklad:
Proudem 1 A nabíjíme kondenzátor 1 F po dobu 1 sekundy*. Napětí roste z 0 na 1 V, dodávaný výkon z 0 na 1 W a nakonec jsme tedy dodali 0,5 J.
Nyní budeme pokračovat tím 1 A po další sekundu: Napětí roste z 1 V, výkon tedy poroste od 1 do 2 W. Přidáme tedy 1,5 J, celkem máme uloženy 2 J.
--------------
*Mimochodem, spolu se závěrem, že se nabije na 1 V je to velmi praktická definice Faradu.
Offline
#3 07. 05. 2020 22:44
- Prokop Ohlídal

- Příspěvky: 26
- Pozice: Student
- Reputace: 1
Re: Energie kondenzátoru
↑ edison:
To znamená, že pokud je něco v první mocnině, tak to nemůžu rozložit?:D
Pořád moc nerozumím tomu, proč je v pořádku dosadit za U, ale za C ne, když by z obojího měl jít dostat výsledek..
Offline
#4 07. 05. 2020 22:57
Re: Energie kondenzátoru
Protože změnit C prakticky znamená vyměnit jeden kondenzátor za jiný.
Samozřejmě je velmi teoreticky možné použít laditelný kondenzátor, ale těch je v moderní elektronice tak 0,00001 %. A to se ještě zpravidla jedná o kapacitní diody, kde ta kapacita závisí na napětí:-)
Offline
#5 07. 05. 2020 23:33
Re: Energie kondenzátoru
Vlastně je požadavek na změnu C přesně totéž, jako chtít v  měnit m. Tedy něco jako vyměnit letící střelu za jinou.
měnit m. Tedy něco jako vyměnit letící střelu za jinou.
A podobně jako u těch kapacitních diod se to v praxi může dít, tentokrát relativisticky, třeba při urychlování částic. :-)
A když ve vzorcích pro kondenzátory prohodíme U a I, dostaneme vzorce pro cívky... a stejný problém bude s L.
Offline
#6 07. 05. 2020 23:36
- Prokop Ohlídal

- Příspěvky: 26
- Pozice: Student
- Reputace: 1
Re: Energie kondenzátoru
↑ edison:
Už rozumím, děkuji moc:)
Offline
#7 08. 05. 2020 15:24
Re: Energie kondenzátoru
Já úplně přesně nerozumím, k čemu směřuje otázka ... ale pokud jde o to, proč se při změně kapacity mění energie lineárně, zatímco při změně náboje kvadraticky, možná taky pomůže se zamyslet nad tím, co se vlastně v kondenzátoru přesně děje.
Máme tedy nabitý kondenzátor - nejlépe tedy dvě rovnoběžné desky, které můžeme přibližovat a oddalovat. Na jedné desce jsou záporné náboje (elektrony) na druhé kladné náboje (atomy, kterým nějaký ten elektron chybí). Desky se navzájem přitahují - protože se přitahují ty náboje co na nich jsou (ale nemohou povrch desky opustit ... to je mimochodem dost základní věc ... a ta síla, co je na deskách drží, není vlastně klasická elektrická síla).
Změna energie kondenzátoru odpovídá práci kterou musíme vynaložit, abychom ho do tohoto stavu dostali. Takže pokud budeme od sebe desky oddalovat, musíme konat práci (desky se přitahují) a energie roste. Pokud jsou desky velké a vzdálenost mezi nimi je malá, přitahují se stále stejnou silou, bez ohledu na vzdálenost (pole mezi nimi je stále stejné ... nemůže se zeslabit, protože velikost pole odpovídá velikosti náboje na deskách). Když je síla konstantní, práce s dráhou lineárně roste (W = F*s). Tudíž roste i energie kondenzátoru.
Jakmile se ovšem desky vzdálí moc, pole se nám začne "vyboulovat" a energie už lineárně neroste. Nicméně ... vztah mezi energií a nábojem je vlastně definice kapacity, takže všechny tyhle nelinearity jsou už schované ve změně kapacity se vzdáleností ... takže v klidu můžeme říct, že s klesající kapacitou nám úměrně roste energie nabitého kondenzátoru.
A teď budeme měnit náboj. Co to znamená? Prostě přenášíme elektrony z jedné elektrody na druhou. Jenže mezi elektrodami je to elektrické pole, takže k přenosu elektronu z kladné elektrody na zápornou potřebujeme zase vykonat práci. Náboj ... to není nic jiného než počet elektronů...(kdybychom používali "správné" jednotky, opravdu by to tak bylo ... běžně se to taky používá, namísto Coulomb se používá jednotka e ... a odpovídá náboji jednoho elektronu). Kdyby se pole neměnilo, byla by práce také úměrná počtu přenesených elektronů ... tedy náboji.
Jenže ono se nám pole mění. S každým elektronem, který přeneseme, bude pole o trochu silnější (protože ty elektrony či jiné náboje nám pole tvoří). Když zdvojnásobíme počet elektronů, zdvojnásobíme i intenzitu el. pole.
Teď už je asi zřejmé, proč je práce úměrná druhé mocnině přeneseného náboje. Jednak práce k přenesení náboje v el. poli závisí na velikosti toho náboje, a jednak velikost toho el. pole samotného také závisí na velikosti už přeneseného náboje.
Samozřejmě, je tam to "už přeneseného" náboje. Musíme to počítat od nuly. Pokud bude v kondenzátoru náboj jeden Coulomb a my přeneseme třeba jeden miliCoulomb, nezvýší se energie o ten milicoulomb na druhou. To né, zvýší se jen o ten milicoulomb. Ale s každým dalším mC bude el. pole trochy vyšší ... až jich přeneseme tisíc, bude pole 2x vyšší ... a k jejich přenosu budeme potřebovat dvojnásobnou energii. Od toho taky pochází ta 1/2...
Já nevím, jestli už umíš počítat integrály, pokud ano, můžu ti to ukázat i matematicky, pokud né, jde to i bez toho pomocí grafů, ale to se mi tu hrozně blbě maluje...
Offline
#8 08. 05. 2020 15:33
- Prokop Ohlídal

- Příspěvky: 26
- Pozice: Student
- Reputace: 1
Re: Energie kondenzátoru
↑ MichalAld:
Děkuji za odpověď, integrály sice počítat neumím, ale nemusíte se dělat s grafem, ještě párkrát si to přečtu a zkusím se nad tím trošku zamyslet a pochopit to, každopádně děkuji moc za Váš čas:)
Offline
#9 08. 05. 2020 19:43 — Editoval MichalAld (08. 05. 2020 19:45)
Re: Energie kondenzátoru
Hele, ono je to nakonec celkem jednoduché, když budeme kondenzátor nabíjet konstantním proudem, bude se napětí rovnoměrně zvyšovat, dle vztahu 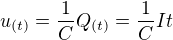
Pro C = 2F a I = 1A by to vypadalo takto:
No a dodaná energie v každém časovém okamžiku je 
Ty trojúhelníčky znamenají změny ... takže energie kondenzátoru se během (krátkého) časového úseky zvýší o U*.I krát délka toho časového úseku. Ten časový úsek ovšem musí být malý ... tak malý, že se během něj napětí skoro nezmění. Nejlépe samozřejmě nekonečně malý.
No a celková energie odpovídá té ploše ohraničené grafem (tou čárou). Pokud chceme tedy spočítat kolik energie jsme do kondenzátoru nacpali od časového okamžiku 0 do časového okamžiku t, bude to 1/2 u(t)I*t. Ta jedna polovina je tam proto že nás zajímá plocha ohraničená tou čárou ... což je trojúhelník...
A protože u(t) = 1\C * I * t, dostáváme, že 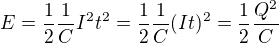
Při odvození jsme předpokládali konstantní proud, aby nám graf vyšel jako přímka, není to ovšem nutné ... energie bude pořád plocha pod grafem, ovšem už to nebude trojúhelník, takže to bez integrálu nespočítáme. Ale výsledek by vyšel stejný.
Offline