Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 13. 05. 2020 14:43
- marnes

- Příspěvky: 11227
Re: goniometrické rovnice
↑ derryos:
sin 2x bych přepsal podle vzorce a řešil rovnici
Jo. A na začátku vás zdravím.
Offline
#5 13. 05. 2020 14:51
Re: goniometrické rovnice
↑ derryos:
Ano, obrázkem to jde velice snadno, otázkou totiž nejsou hodnoty kořenů rovnice, nýbrž jen počet řešení. Takže až ten sin 2x nakreslíš lépe, uvidíš hned bez počítání počet řešení.
Offline

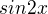 pomocí nějakého vzorečku a pak pokračovat dál.
pomocí nějakého vzorečku a pak pokračovat dál. takže by to bylo
takže by to bylo 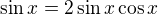 a pak vydělím sinx
a pak vydělím sinx 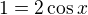 ale dál nevím
ale dál nevím