Matematické Fórum

Ahoj ↑ anddry97:

to co robis je zda sa prakticky pouzitie vety o implicitnej funkcii a k stacionarnym bodom ta to privedie,
kedze zaviest v takomto priklade implicitnu funkciu v smere osi x alebo y bude zrejme ekvivalentne
hladaniu parcialnej derivacie v smere vektora (1,0) alebo (0,1), t.j. podla premennej x a podla premennej y.

EDIT: Nakoniec nie vzdy, vid nizsie ↑ Brano:

Pouzitie takehoto postupu je ale aj tak nevyhodne z niekolkych dovodov.

1) je to zbytocna praca navyse a komplikovanejsi sposob ako sa dopracovat k stacionarnym bodom,
    prakticky si pridavas niekolko zbytocnych krokov

2) pre dalsie vysetrovanie stacionarnych bodov cez hessian aj tak potrebujes spocitat parcialne derivacie
    (v tvojom postupe figuruju ako citatele zlomkov pri osamostatneni ,,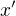
     takze je to ozaj pocitanie toho isteho len komplikovanejsie)

3) pozor, na volbe nezavislej premennej zalezi, len to nie je vidiet v priklade ktory si ponukol
    mozes si vsimnut ze funkcia je symetricka co sa tyka premennych

Děkuji oboum :)