Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 15. 05. 2020 07:57
Re: Příklad na komplexní čísla
↑ derryos:
Samozřejmě, že můžeš. Je otázka, jak ti to pomůže. Vzorec 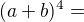 moc lidí nezná, zatímco
moc lidí nezná, zatímco 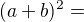 je učivo základní školy.
je učivo základní školy.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 15. 05. 2020 08:34
Re: Příklad na komplexní čísla
↑ zdenek1:
to znamená že to mám roznásobit podle vzorce 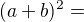 a pak zase z tý 8 udělat
a pak zase z tý 8 udělat 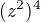 a pak zase
a pak zase 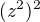 a pak
a pak 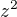 ?
?
Offline
#6 15. 05. 2020 08:59
#8 15. 05. 2020 09:14
Re: Příklad na komplexní čísla
↑ derryos:
Ne, ale měl bys vědět nazpaměť, že 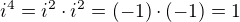
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#9 15. 05. 2020 10:43
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Příklad na komplexní čísla
↑ derryos:
Mne ta tvoje myslenka pocitat 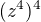 prijde uplne v pohode. Pokud ma clovek geometrickou predstavu mocneni komplexnich cisel, tak je videt, ze
prijde uplne v pohode. Pokud ma clovek geometrickou predstavu mocneni komplexnich cisel, tak je videt, ze 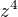 bude realne cislo, takze pocitat 4. mocninu je vlastne pekne.
bude realne cislo, takze pocitat 4. mocninu je vlastne pekne.
A navic se 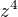 da pocitat jako
da pocitat jako 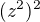 , coz uz je potom stejne jako to, co pise zdenek1 nebo Cheop.
, coz uz je potom stejne jako to, co pise zdenek1 nebo Cheop.
Ohledne komplexnich cisel si nepotrebujes pamatovat nic jineho nez ze  . Vsechno ostatni z toho odvodis. Napriklad ten posledni vypocet od zdenka.
. Vsechno ostatni z toho odvodis. Napriklad ten posledni vypocet od zdenka.
Je ale pravdou, ze hodne lidi si mocniny cisla i vicemene pamatuje (nebo je umi pocitat bleskove), protoze se to deje dost casto a navic to je vlastne jednoduche. Kdyz si spocitas nekolik prvnich mocnin 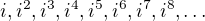 , zjistis, ze se tam vlastne porad dokola toci ctyri hodnoty.
, zjistis, ze se tam vlastne porad dokola toci ctyri hodnoty.
Offline
#11 15. 05. 2020 13:33 — Editoval Ferdish (15. 05. 2020 13:33)
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Příklad na komplexní čísla
↑ derryos:
Pretože ktorákoľvek  -tá mocnina imaginárnej jednotky
-tá mocnina imaginárnej jednotky  , kde
, kde  je násobok štvorky je rovná (reálnej) jednotke.
je násobok štvorky je rovná (reálnej) jednotke.
Nie je tam uvedený medzikrok, kde mocnina 87 je rozložená ako 84+3 a 84 je násobok štvorky, teda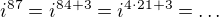
Offline
#12 15. 05. 2020 13:34 — Editoval david_svec (15. 05. 2020 13:37)
- david_svec
- Příspěvky: 435
- Pozice: student
- Reputace: 13
Re: Příklad na komplexní čísla
↑ derryos:
Když 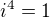 , tak
, tak 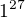 je pořád jedna. Jednička umocněná na jakoukoliv mocninu je pořád jedna. :-)
je pořád jedna. Jednička umocněná na jakoukoliv mocninu je pořád jedna. :-)
EDIT: kolega Ferdish rychlejší, ale nechám to tu už. :-)
Offline

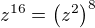
 ?
?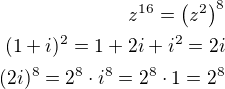
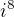 je 1?
je 1?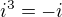 a a že
a a že 