Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Základní škola
- » Úhel mezi dvěma stranami dvanáctiúhelníku (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 03. 2012 17:28
Úhel mezi dvěma stranami dvanáctiúhelníku
Zvládl byste mi někdo prosím poradit, jak vypočítat, jak velký úhel svírají dvě strany dvanáctiúhelníku? Počítá se na podobném principu i např. osmiúhelník nebo desetiúhelník?
Offline
- (téma jako vyřešené označil(a) Zuzka.s)
#2 29. 03. 2012 17:37 — Editoval frank_horrigan (29. 03. 2012 17:38)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Úhel mezi dvěma stranami dvanáctiúhelníku
Ahoj,
ano, počítá, obecný vzorec pro výpočet vnitřního úhlu pravidelného mnohoúhelníku zní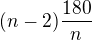 ve stupních, nebo
ve stupních, nebo 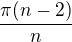 radiánů ,
radiánů ,  vyjadřuje počet stran daného mnohoúhelníku
vyjadřuje počet stran daného mnohoúhelníku
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#5 13. 05. 2020 14:56 — Editoval Bahner Filip (13. 05. 2020 15:37)
- Bahner Filip

- Zelenáč
- Příspěvky: 1
- Škola: SPŠ STAVEBNÍ OSTRAVA
- Reputace: 0
Re: Úhel mezi dvěma stranami dvanáctiúhelníku
↑ Zuzka.s:
Myslim, že k tomuto laicky nepotřebuješ žádný vzorec. Kružnice má 360 stupňů. Součet trojúhelníku má 180 stupňů, to vsichni si pamatujeme. Pokud je strana 12 uheln základna, pak je složen z dvanácti rovnoramenych trojúhelníku, že? Stejně trojúhelníky tedy ve vrcholech tohoto trojuhelniku (myslím úhly u středu S) při středu svírá tedy 12 X úhel.... Tedy 360/12, což je 30 stupňů.....
A jelikož se jedná o rovnoramenne trojúhelníky.... Tedy o 2 stejná ramena (délky poloměru kružnice opsane, neboli Úsečky SA, SB,... SL (n pořadí v abecedně dle počtu stran) jsou úhly vždy mezi polomerem a stranou stejné .... Tedy polovina z 180 minus onen vrcholový 30 stupňů = (180-30)/2=150 /2 =75 stupnu..... vychází, že tento úhel je 75 stupňů.
Jedna se ale o úhel mezi polomerem a stranou uhelnik, ktery vlastně svira osu úhlu vašeho dotazů, tedy dvou stran mezi sebou.... Což je X 2. 75 opět x 2 =150 stupňů.(...tady jde o nahodu s dvemi zbývajícím úhly 180 minus 30 =150? Nechám na vás ať můžete přemýšlet....) Zamyšlení, zda platí i to, jestli v licho nebo i sudo n-uhelniku opět půli poloměr úhel mezi stranami.... Co myslíte?
Zhrnuti:
Jde si to prostě odvodit bez vzorce, když si rozložit n uhelnik na jednotlivé rovnoramenne trojúhelníky, jejichž součet úhlu je vždy 180. Při středu je prostě úhel roven 360 deleno počet stran (úhlu) a dvemi úhly tvořene rovnostranmeho trojuhelniku, které jsou totožné (2 stranami ze středu do vždy dvou sousedicich vrcholu onoho nuhelniku)
Offline
#6 13. 05. 2020 15:58
- misaH
- Příspěvky: 13459
Re: Úhel mezi dvěma stranami dvanáctiúhelníku
↑ Bahner Filip:
To sa to debatuje s niekým spred 8 rokov...
Offline
#7 15. 05. 2020 15:39 Příspěvek uživatele Zuzka.s byl skryt uživatelem Zuzka.s.
#8 15. 05. 2020 15:40
Re: Úhel mezi dvěma stranami dvanáctiúhelníku
↑ Bahner Filip: Jé, to jsem nečekala, kde a kdy se mi ještě lidé budou ozývat! No, děkuji za vysvětlení. Když jsem to psala, bylo mi 15, to je hezké, se takhle vrátit v čase k příspěvku, o kterém jsem ani nevěděla, že ještě někde stojí. Mějte se hezky!
Offline
Stránky: 1
- Hlavní strana
- » Základní škola
- » Úhel mezi dvěma stranami dvanáctiúhelníku (TOTO TÉMA JE VYŘEŠENÉ)


 tedy pro osmičku, desítku i dvanáctku. Ten vzorec se dá logicky odvodit.
tedy pro osmičku, desítku i dvanáctku. Ten vzorec se dá logicky odvodit.