Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 05. 2020 18:21
- Vladimir9O

- Příspěvky: 104
- Reputace: -1
Adherze/přilnavost při rozjezdu stroje.
K čemu je tak podstatná a jak s ní pracovat?
Offline
#2 09. 05. 2020 18:28 — Editoval edison (09. 05. 2020 18:31)
Re: Adherze/přilnavost při rozjezdu stroje.
Když je překročen adhezní poměr, poháněná kola se utrhnou od povrchu a začnou "hrabat".
Podstatné to může bejt hodně: Třeba tramvaj má kolem 0,1, takže kdyby někdo za půl miliardy postavil trať do kopce se sklonem 15 %, tak tam prostě nepůjde jezdit:-)
Offline
#3 10. 05. 2020 11:11
- Vladimir9O

- Příspěvky: 104
- Reputace: -1
Re: Adherze/přilnavost při rozjezdu stroje.
Dobře, takže adheze je vyjádření dotyku mezi kolem a věci po které to kolo jezdí.
Ale jako co s tím? Synovi bylo řečeno nastuduj adhezi... ale co a jak?
Offline
#4 10. 05. 2020 13:06 — Editoval edison (10. 05. 2020 13:06)
Re: Adherze/přilnavost při rozjezdu stroje.
Mějme nějakou věc (bez kol) a zkusme jí táhnout po zemi. Věc je přitlačována přítlačnou silou Fp=mg a zjistíme, že k tažení potřebujeme tažnou sílu Ft, jinak se věc nehne. Platí: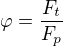 přičemž
přičemž  je adhezní poměr pro kontakt materiálu taženého tělesa a materiálu podkladu.
je adhezní poměr pro kontakt materiálu taženého tělesa a materiálu podkladu.
Např. ocel-ocel má v řádu 0,1, naopak třeba guma-asfalt má v řádu 10. Proto se může auto rozjíždět/brzdit poněkud snadněji, než tramvaj.
Offline
#5 16. 05. 2020 11:30
- Vladimir9O

- Příspěvky: 104
- Reputace: -1
Re: Adherze/přilnavost při rozjezdu stroje.
https://ibb.co/g3cRFjS
OK, ještě prosím:
1. tažná síla je taky F=m . g?
2. když mám kolové těleso (třeba to auto) tak ty kola hrají ve vzorci nějakou úlohu? Že bylo zdůrazňováno, že "mějme nějakou věc (bez kol)..."
Offline
#7 16. 05. 2020 12:01
- Vladimir9O

- Příspěvky: 104
- Reputace: -1
Re: Adherze/přilnavost při rozjezdu stroje.
Jak "překročení φ"? φ je nějaká konstanta, že se dá "překročit"?
Offline
#9 16. 05. 2020 12:12
Re: Adherze/přilnavost při rozjezdu stroje.
Ještě pokračování sání:
Po té, co je odtrhneš a začnou se pohybovat, začne platit:
Ft = Ftr + Fz
Ft je pořád tvoje tažná síla
Ftr je třecí síla
Fz je síla působící zrychlení
Pro Ftr platí stejný vzorec jako pro adhezi, ale místo adhezního činitele Fí, máme činitel smykového tření, který píšeme jako µ (malé řecké písmenko mí) a je menší než Fí.
zbývající síla Fz se využije na zrychlování Fz = m.a přičemž a je výsledné zrychlení.
Zajímavé je, že na wiki o tření:
https://cs.wikipedia.org/wiki/T%C5%99en … dové_tření
zavádějí ještě klidové tření, což si myslím (ale nejsem si 100% jist), že je totéž jako adheze.
Offline
#11 16. 05. 2020 12:21 — Editoval edison (16. 05. 2020 12:21)
Re: Adherze/přilnavost při rozjezdu stroje.
↑ Vladimir9O:Ano, φ a µ jsou konstanty pro adhezi a smykové tření a obě závisejí na vlastnostech materiálů.
O φ jsem přeci psal už tady: ↑ edison:
Offline
#12 17. 05. 2020 10:25
- Vladimir9O

- Příspěvky: 104
- Reputace: -1
Re: Adherze/přilnavost při rozjezdu stroje.
edison napsal(a):
Ještě pokračování sání:
Po té, co je odtrhneš a začnou se pohybovat, začne platit:
Ft = Ftr + Fz
Ft je pořád tvoje tažná síla
Ftr je třecí síla
Fz je síla působící zrychlení
Pro Ftr platí stejný vzorec jako pro adhezi, ale místo adhezního činitele Fí, máme činitel smykového tření, který píšeme jako µ (malé řecké písmenko mí) a je menší než Fí.
zbývající síla Fz se využije na zrychlování Fz = m.a přičemž a je výsledné zrychlení.
Zajímavé je, že na wiki o tření:
https://cs.wikipedia.org/wiki/T%C5%99en … dové_tření
zavádějí ještě klidové tření, což si myslím (ale nejsem si 100% jist), že je totéž jako adheze.
Okej, a co je teda lepší? Když jede tramvaj (ocel/ocel) po kolejnicích, nebo když jeden vlak s ocelovejma kolama po ocelových kolejnicích?
Dobře, a jak do toho do adhezi napasovat? Do těch vzorců?
"Pokud je těleso taženo na provaze, vláknu nebo lanku, pak říkáme, že je lanko napínáno.Těleso je
taženo silou T, která směřuje podél lanka ven z objemu tělesa a její působiště je v místě úchytu lanka.
Tuto sílu budeme nazývat tahovou silou lanka." https://www.aldebaran.cz/~blahova/F1KME/13.pdf
↑ Tam vzorec není.
U třecí síly tomu rozumím:
Konstantou přímé úměrnosti, která vyjadřuje závislost velikost třecí síly na velikosti normálové síly, je koeficient smykového tření,který budeme značit ft.
Koeficient smykového tření se určuje experimentálně pro materiály, z nichž je
vyrobeno pohybující se těleso a podložka a je bezrozměrnou veličinou.
F⃗t = −ft Fn ⃗τ0
kde ⃗τ0 je jednotkový vektor ve směru pohybu tělesa (tečný k trajektorii pohybu).
ft teda získám z tabulek.
Ten " ⃗τ0" ovšem nevím kde získat.
Offline
#13 17. 05. 2020 11:03
Re: Adherze/přilnavost při rozjezdu stroje.
Vladimir9O napsal(a):
Okej, a co je teda lepší? Když jede tramvaj (ocel/ocel) po kolejnicích, nebo když jeden vlak s ocelovejma kolama po ocelových kolejnicích?
Klasický vlak je na tom hůř, protože hnaná kola jsou jen na lokomotivě. Proto musí být lokomotiva velmi těžká a normy pro vlakové koleje požadují menší maximální sklon. Při mechanickém brždění jsou na tom stejně, brzdí všechna kola, i na vagonech.
Dobře, a jak do toho do adhezi napasovat? Do těch vzorců?
Kterých?
"Pokud je těleso taženo na provaze, vláknu nebo lanku, pak říkáme, že je lanko napínáno.Těleso je taženo silou T, která směřuje podél lanka ven z objemu tělesa a její působiště je v místě úchytu lanka.
Tuto sílu budeme nazývat tahovou silou lanka." https://www.aldebaran.cz/~blahova/F1KME/13.pdf
↑ Tam vzorec není.
Těch je totiž víc, podle okolností, zejména toho, kde bude lanko upnuté (nebo jich nebude víc, ale bude to nějaká složitost s integrálem). To je vidět třeba na tý wiki. Tomu jsem se já vyhnul tím, že jsem psal nejjednodušší vztahy pro vodorovné tažení tělesa zanedbatelné výšky proti délce. Jakmile začneme řešit nějaké jiné těleso než tenkou placku, začne se to bohužel komplikovat a do vzorců nalezou siny, kosiny a další breberky:-)
U třecí síly tomu rozumím:
Konstantou přímé úměrnosti, která vyjadřuje závislost velikost třecí síly na velikosti normálové síly, je koeficient smykového tření,který budeme značit ft.
Koeficient smykového tření se určuje experimentálně pro materiály, z nichž je
vyrobeno pohybující se těleso a podložka a je bezrozměrnou veličinou.
F⃗t = −ft Fn ⃗τ0
kde ⃗τ0 je jednotkový vektor ve směru pohybu tělesa (tečný k trajektorii pohybu).
ft teda získám z tabulek.
Ten " ⃗τ0" ovšem nevím kde získat.
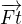 je vektor. Má velikost a směr. Protože v druhé části vzorce se to nehodí, byl směr "vyhozen" do jednotkového vektoru
je vektor. Má velikost a směr. Protože v druhé části vzorce se to nehodí, byl směr "vyhozen" do jednotkového vektoru 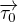 . Ten má velikost 1 a jako užitečnou informaci obsahuje jen směr. Tohle asi pro dítě na základce potřeba nebude:-)
. Ten má velikost 1 a jako užitečnou informaci obsahuje jen směr. Tohle asi pro dítě na základce potřeba nebude:-)
Offline
#14 17. 05. 2020 14:30
- Vladimir9O

- Příspěvky: 104
- Reputace: -1
Re: Adherze/přilnavost při rozjezdu stroje.
Dobře, a jak do toho do adhezi napasovat? Do těch vzorců?
Kterých?
Do těch vzorců pro rozjezd a pohyb "vlaku"
Offline
#15 17. 05. 2020 14:40 — Editoval edison (17. 05. 2020 14:42)
Re: Adherze/přilnavost při rozjezdu stroje.
Jako okrajovou podmínku:
Fo .. síla na obvodu kola
Ft .. přítlačná síla
µ0 .. adhezní poměr, alias součinitel statického tření (alias φ co jsem našel, když jsem poprvé hledal písmenka používaná u adheze)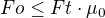
Je-li splněna, kolo nehrabe při rozjezdu, neklouže při brždění.
Offline
#16 17. 05. 2020 14:50
- Vladimir9O

- Příspěvky: 104
- Reputace: -1
Re: Adherze/přilnavost při rozjezdu stroje.
A tu sílu na obvodu kola vezmu kde?
Offline
#17 17. 05. 2020 14:57
Re: Adherze/přilnavost při rozjezdu stroje.
1. Např. vypočítám z momentu motoru, převodového poměru, počtu tímto motorem hnaných kol a poloměru kola.
2. Nebo ze zrychlení, hmotnosti vlaku a celkového počtu hnaných kol (počtu bržděných kol).
Obráceně proti (2) pak lze stanovit, jaké max zrychlení vlak zvládne při rozjezdu a brždění.
Offline
#18 17. 05. 2020 15:30
- Vladimir9O

- Příspěvky: 104
- Reputace: -1
Re: Adherze/přilnavost při rozjezdu stroje.
"počtu hnaných kol (počtu bržděných kol)."
U tohohle mi kámoš říkal, že "hnána" jsou kola lokomotivy, ale brzdí se i kolama vagonu.
Offline
#19 17. 05. 2020 16:02
Re: Adherze/přilnavost při rozjezdu stroje.
Přesně tak, proto pro rozjezd a brždění vyjdou jiné max. hodnoty zrychlení.
Kromě kámoše jsem o tom psal i já tady: ↑ edison:
... pak máme ještě "vláčky motoráčky", kde jsou motory všude, tam je to stejné.
A tramvaje zas mají navíc i kolejnicové brzdy, které se nezávisle na kolech "přicucnou" ke kolejím cca stejnou silou, jako odpovídá nominální hmotnosti tramvaje a tím mohou cca zdvojnásobit brzdné zrychlení. Zapínají se, když řidič sešlápne brzdu až dolů. Má to dva stupně, napřed se zapnou zadní, pak přední, takže je to trochu "plynulé" a lidi obvykle nepadaj:-)
Offline
#20 17. 05. 2020 16:13
Re: Adherze/přilnavost při rozjezdu stroje.
Ještě jedna poznámka: Specialita sama pro sebe jsou zatáčky. Tam se samozřejmě délka dráhy levých a pravých kol liší...
U aut to se to musí řešit buď diferenciálem, nebo levými a pravými motory (jen v elektromobilech).
U kolejnicových prostředků se to neřeší, hřeší se na to, že díky malé adhezi to může na jedné straně (zpravidla vnitřku zatáčky) "beztrestně" prokluzovat. Proto v zatáčkách skřípou a oblouky se často musí vyvařovat a brousit.
Offline
#21 17. 06. 2020 17:06
- Vladimir9O

- Příspěvky: 104
- Reputace: -1
Re: Adherze/přilnavost při rozjezdu stroje.
Dobře, u aut diferenciálem, jak se to ale řeší z matematického úhlu pohledu?
Offline
#22 17. 06. 2020 20:27 — Editoval Aleš13 (17. 06. 2020 20:42)
Re: Adherze/přilnavost při rozjezdu stroje.
edison napsal(a):
JU kolejnicových prostředků se to neřeší, hřeší se na to, že díky malé adhezi to může na jedné straně (zpravidla vnitřku zatáčky) "beztrestně" prokluzovat. Proto v zatáčkách skřípou a oblouky se často musí vyvařovat a brousit.
Omlouvám se, že do toho off-topic kecám, ale viděl jsem nepřesnost a nedá mi to :-) V obloucích (zatáčky na železnici nejsou) železniční podvozky skřípou proto, že se okolky třou o boky kolejnic. Samotná kola se po kolejnících odvalují teoreticky bez skluzu, protože jízdní plochy kol jsou kuželové, v obloucích je zvětšený rozchod kolejnic a dvojkolí se tudíž posune tak, že se po vnější kolejnici odvaluje po větším průměru. Na přímé trati se za ideálních podmínek kola díky kuželovitosti (a příčnému sklonu kolejnic) naopak sama srovnají tak, aby se odvalovala po stejných průměrech a okolky se kolejnic nedotýkají (ve skutečnosti ještě konají dvojkolí příčné harmonické kmity s vlnovou délkou závislou na kuželovitosti a nezávislou na rychlosti jízdy).
Offline
#23 17. 06. 2020 20:40 — Editoval Aleš13 (17. 06. 2020 20:40)
Re: Adherze/přilnavost při rozjezdu stroje.
↑ Vladimir9O:
Viz moje připomínka výše, u normálně jedoucího vlaku nedochází ke smykovému tření, takže stačí počítat adhezi (která je číselně vyšší). Samozřejmě jakmile by se kola vlaku zastavila ač by vlak byl v pohybu, nebo se točila a vlak stál, muselo by se použít smykové tření.
Offline