Matematické Fórum

jansed · 12. 01. 2008 17:45

Mohl by mi někdo prosím poradit s tímto příkledam........

Ke třem vektorům a = (2, 1, 3), b = (3, 2, 5), c = (-1, -1, 4) byl přidán čtvrtý d = (-5, -4, -9). Co můžete říci o jeho poloze vůči prvým třem?

Saturday · 12. 01. 2008 20:44

Nezjistil jsem, že by měli nějakou speciální polohu, když uděláš skalární součiny, tak zjistíš, úhel mezi vektory (kolmé žádné nejsou)..

Jsi si jist zadáním?

jansed · 13. 01. 2008 10:52

↑ Saturday:
Zadání je určitě dobře,ještě jsem si to kontroloval.....

nika.v · 15. 01. 2008 13:51

Tak je s nimi lineárně nezávislý :-) asi

jansed · 24. 01. 2008 20:41 — Editoval jansed (24. 01. 2008 20:43)

Ten výpočet úhlu by vypadal asi takto?????

Ale nevím jak dál.... :-(
Jak dokázat tu lineární nezávislost.

jelena · 24. 01. 2008 21:14

Tedy linearni algebra neni muj oblibeny obor, ale nerozumi se to jako pozadavek vyjadrit vektor d jako linearni kombinaci vektoru a, b, c (tato trojice jsou totiz linearne nezavisle) ?

Marian · 24. 01. 2008 21:32

Souhlasil bych s jelenou.

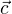Jednoznacnou informaci o vektoru $\vec{d}$ vuci vektorum $\vec{a}$ , $\vec{b}$ a $\vec{c}$ nam da prave vyjadreni tohoto vektoru pomoci trech posledne uvedenych.

Navic bzch si dovolil malou formalni poznamku k prispevku od janseda. Ta tri rovnitka zcela vpravo by mela vypadat jinak. Totiz mas dve moznosti, jak to opravit: bud je nahradit znakem $\dot{=}$ nebo $\approx$ .

jansed · 25. 01. 2008 07:14

Takže to vyjadření úhlů vektorů je správně vypočteno?

A jak dokážu, že jsou lineárně nezavislé???

plisna · 25. 01. 2008 08:30

dej vsechny vektory do matice (budes mit matici 4x3) a uprav ji na schodovity tvar, pocet nenulovych radku udava pocet nezavislych vektoru (v tvem pripade vyjde jeden nulovy radek, tj jeden vektor je linearne zavisly = lze jej zapsal linearni kombinaci ostatnich)

Matematické Fórum

#1 12. 01. 2008 17:45

Vektory

#2 12. 01. 2008 20:44

Re: Vektory

#3 13. 01. 2008 10:52

Re: Vektory

#4 15. 01. 2008 13:51

Re: Vektory

#5 24. 01. 2008 20:41 — Editoval jansed (24. 01. 2008 20:43)

Re: Vektory

#6 24. 01. 2008 21:14

Re: Vektory

#7 24. 01. 2008 21:32

Re: Vektory

#8 25. 01. 2008 07:14

Re: Vektory

#9 25. 01. 2008 08:30

Re: Vektory

Zápatí