Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Základní škola
- » Slovní úlohy o společné práci a pohybu (TOTO TÉMA JE VYŘEŠENÉ)
#2 17. 03. 2009 17:00 — Editoval ttopi (17. 03. 2009 17:07)
Re: Slovní úlohy o společné práci a pohybu
Tak sem s těma úlohama :-)
Pokud myslíš obecný postup, tak nejprve je dobré si výkon jednotlivých účastníků převést na výkon za hodinu. Například trvá-li někomu postavit zeď za 4 hodiny, znamená to, že za 1 hodinu postaví 1/4 zdi, to je ti doufám jasné. Když si to takto přepíšeš, nezbývá nic lepšího, než si napsat rovnici, kde na pravé straně bude 1, která značí 1 celek a nalevo budou zlomky,kde v čitateli je X což je hledaný čas a ve jmenovateli bude v našem případě ta 4. Tyto zlomky se sčítají.
Dám jednoduchý příklad:
1 delník postaví zeď za 4 hodiny a druhý za 2 hodiny. Za jak dlouho postaví zeď společně?
Napíšeš si hodinové výkony dělníků, tedy:
1.dělník......1/4 za hodinu
2.dělník......1/2 za hodinu
Pak utvoříš rovnici, jak jsem říkal:
Z takovéto rovnice je už pak snadné zjistit, jak dlouho jim to bude trvat, tedy čemu se rovná X. Tento postup je ten nejzákladnější. Samozřejmě pak jsou úlohy zadány tak, že jeden pracuje déle než druhý a podobně, to je pak mírně složitější.
oo^0 = 1
Offline
#4 20. 03. 2009 13:42 — Editoval Rumburak (20. 03. 2009 14:45)
Re: Slovní úlohy o společné práci a pohybu
↑ loolly: Tak třeba:
Vzdálenost z A do B je 15 km.
V 8"00 vyjel z A do B cyklista stálou rychlostí 20 km/hod.
Kdy nejpozději musí za cyklistou vyjet automobilista stálou rychlostí 90 km/hod, aby cyklistu dostihl nejpozději v okamžiku, když dojede do B?
Řešení - nejprve úsudkem např. takto:
Cyklista za 1 hod. ujede 20 km.
Dráha 15 km z A do B je 3/4 z 20-ti, takže cyklista dojede do B za 3/4 hod. , tj. v 8"45 .
Tedy automobilista musí vyjet tak, aby se dostal do B nejpozději v 8"45 .
Při rychlosti 90 km/hod. ujede automobil dráhu 15 km z A do B za 1/6 hodiny (neboť 90 = 6*15) , tedy za 10 minut.
Aby dostihl cyklistu nejpozději v 8"45 , musí vyjet nejpozději v 8"35.
Nyní pomocí rovnice
Nejprve určíme neznámou. Často (i když ne vždy) bývá výhodné určit jako neznámou přímo to, na co se ptáme, zkusíme to také, tedy
x ... okamžik v hodinách (i když to obecně nebude celé číslo), kdy nejpozději musí automobil vyjet z A, aby ještě dostihl cyklistu,
tj. aby dostihl cyklistu v okamžiku jeho příjezdu do B.
Dále vyjádříme (případně pomocí neznámé) některé údaje, které mohou být pro výpočet důležité. Umět odhadnout, co bude důležité,
je otázkou zkušenosti:
15/90 ... doba jízdy automobilisty z A do B,
20*(x - 8) .... vzdálenost od A, kterou v okamžiku x již ujel cyklista.
15 - 20*(x - 8) ... vzdálenost, která v okamžiku x cyklistovi zbývá do B,
tuto vzdálenost cyklista ujede za dobu (15 - 20*(x - 8)) / 20 hod.
Tato doba musí být stejná, jako doba jízdy automobilisty z A do B, takže sestavíme rovnici
(15 - 20*(x - 8)) / 20 = 15/90
3/4 - (x - 8) = 1/6 ,
x - 8 = 3/4 - 1/6,
x = 8 + 3/4 - 1/6 = 8 hod. + 45 min. - 10 min = 8"35 .
Metoda pomocí rovnice bývá ve srovnání s úsudkem poněkud kostrbatá, ale může vést k cíli i tam, kde
zadání úlohy je pro řešení úsudkem příliš složité. "Kostrbatost" lze snížit zavedením dalších neznámých,
za každou neznámou pak musí být odvozene jedna rovnice nezávislá na ostatních rovnicích.
EDIT. Základem pro tyto úlohy je znát fyzikální vzorečky V = S / T resp. S = V * T resp. T = S / V ,
kde S je dráha, kterou za dobu T urazí bod pohybující se stálou rychlostí V.
Offline
#5 20. 03. 2009 14:17 — Editoval Cheop (20. 03. 2009 14:22)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Slovní úlohy o společné práci a pohybu
↑ Rumburak:
Nešlo by to takto? (možná je to pro tazatele pochopitelnější)
Čas cyklisty na dráze 15 km při rychlosti 20 km/h je: 
Čas automobilisty je na dráze 15 km při rychlosti 90 km/h 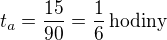
Rozdíl  bude čas, o který může automobilista vyjet později než cyklista tak, aby byli oba v cílovém místě stejně. tj:
bude čas, o který může automobilista vyjet později než cyklista tak, aby byli oba v cílovém místě stejně. tj:
Když tedy cyklista vyjel v 8:00 hodin, potom automobilista může nejpozději vyjet v 8:35 hodin
Zapsat do rovnice by to šlo tedy takto: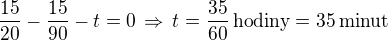
Nikdo není dokonalý
Offline
#9 21. 03. 2009 15:49 — Editoval ttopi (21. 03. 2009 16:00)
Re: Slovní úlohy o společné práci a pohybu
Ahoj.
Jestliže gepard antilopu chytil, znamená to, že obě zvířata měla v době setkání stejnou dráhu a toho využijem. (Ten gepard sice musí oběhnout v době honění více, ale od jeho počátku do okamiku chycení je dálka těchto 2 bodů stejná pro obě zvířata)
Z Fyziky: 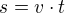
 a vzdálenost mezi zvířaty je 120m, tedy 0,12km.
a vzdálenost mezi zvířaty je 120m, tedy 0,12km.
Teď jen dát do rovnosti co je třeba. K dráze antilipy, kterou uběhla rychlostí 72km/h po dobu těch 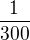 h je třeba přičíst těch 0,12km. Takže:
h je třeba přičíst těch 0,12km. Takže: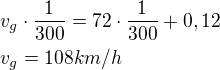
EDIT: Omlouvám se, původně jsem počítal s časem 12 minut, ale je to 12 sekund, teď už je to správně.
oo^0 = 1
Offline
#10 21. 03. 2009 15:50
Re: Slovní úlohy o společné práci a pohybu
↑ ttopi:Nemohl by si mi taky pomoct s touto ulohou???když gepard zacal pronasledovat antilopu,byla mezi nimi vzdálenost 120m.Přestože antilopa utíkala rychlostí 72 km/h,gepard ji dohonil za 12 sekund. Jakou rychlostí gepard běžel?Rychlost vyjádřete v km/h
Offline
#13 21. 03. 2009 16:10
Re: Slovní úlohy o společné práci a pohybu
Však říkám. Když je úloha typu, že někdo někoho dohonil, vždy se dávají do rovnosti dráhy. Nalevo je dráha geparda, který má rychlost v_g a běží 0,2h. Nalevo je čas antilopy, která běží rychlostí 72km/h a také 0,2h. To 0,12 je tam proto, že měla náskok 120 metrů, což se musí převést na km. Z této rovnice pak rychlost geparda v_g lehce spočteš.
oo^0 = 1
Offline
#15 21. 03. 2009 17:56
Re: Slovní úlohy o společné práci a pohybu
antilopa běžela rychlostí 72 km/h, to znamená, že za 12 sekund (než ji doběhl gepard) uběhla vzdálenost  km (těch 3600 je vyjádření hodiny v sekundách). Gepard uběhl jednak těch 120 m (0,12 km) plus 0,24 km=0,36 km
km (těch 3600 je vyjádření hodiny v sekundách). Gepard uběhl jednak těch 120 m (0,12 km) plus 0,24 km=0,36 km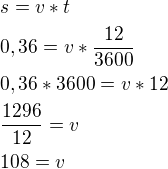
Gepard běžel rychlostí 108 km/h.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#16 22. 03. 2009 14:15
Re: Slovní úlohy o společné práci a pohybu
↑ m.k.:
Úplně jednoduše takto:
72 km/h = 20 m/s (72/3.6 = 20)
Antilopa za 12 sekund než ji gepard dostihne uběhne: 20*12 = 240 m
Gepard za 12 sekund musí uběhnout o 120 m více tj. 240 + 120 =360 m
Musí tedz běžet rychlostí:
v = 360/12 = 30 m/s
30*3,6 = 108 km/h
Rychlost geparda je 108 km/h.
Offline
#17 25. 05. 2020 08:57
Re: Slovní úlohy o společné práci a pohybu
Ahoj vypočte mi někdo prosím tuto úlohu :
Antilopa byla vzdálena od geparda 100 m. V okamžiku, když se za ní gepard rozběhl, dala se
na útěk. Gepard běžel průměrnou rychlostí 1 200 m za 1 minutu (72 km/h)
a antilopa 700 m za 1 minutu (42 km/h). Za kolik sekund byl schopen gepard dohonit antilopu?
Offline
#18 25. 05. 2020 08:59
Re: Slovní úlohy o společné práci a pohybu
A také bych potřebovala pomoc tuto ulohou:
Na silnici v místě H došlo ve 13 h 30 min k dopravní nehodě. Nemocnice, jejíž vzdušná
vzdálenost od místa H byla 30 km, obdržela o této nehodě informaci mobilním telefonem
ve 13 h 35 min. Pět minut nato odstartoval z nemocnice vrtulník Eurocopter s lékaři záchranné
služby. K místu H letěl vrtulník přímočaře průměrnou rychlostí 150 km/h. V kolik hodin a minut
mohli lékaři poskytnout raněným první pomoc?
Offline
#19 25. 05. 2020 09:35
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Slovní úlohy o společné práci a pohybu
↑ Klkt:
Rozdíl rychlostí gepard - antilopa je:
20-35/3=25/3 m/s
Touto rychlostí se gepard přibližuje k antilopě a musí urazit o 100 m více než antilopa tedy
čas za který antilopu dosthne je: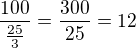 vteřin
vteřin
Nikdo není dokonalý
Offline
#20 25. 05. 2020 09:40 — Editoval Cheop (25. 05. 2020 10:17)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Slovní úlohy o společné práci a pohybu
↑ Klkt:
Vrtulník uletí 30 km rychlostí 150 km/h za 1/5 hodiny
Než posádka vrtulníku mohla vzlétnout uběhlo od nehody 10 minut.
Úlohu si už dopočítej.
PS proč ty úlohy píšeš už do uzavřeného tématu?
Příště si založ vlastní téma.
Nikdo není dokonalý
Offline
Stránky: 1
- Hlavní strana
- » Základní škola
- » Slovní úlohy o společné práci a pohybu (TOTO TÉMA JE VYŘEŠENÉ)
